Category:Auditory Image
From CNBH Acoustic Scale Wiki
Roy Patterson
When an event occurs in the world around us, say a vocalist sings the opening bars of Amazing Grace, information about the event is transmitted to us by light waves and sound waves emanating from the vocalist. Our eyes create a sequence of visual images of the event, our ears form a sequence of auditory images of the event, and the brain combines these image sequences, with any other sensory input, to produce our initial experience of the event. In parallel, the brain interprets the event with respect to the scene in which it occurs, and in terms of stored knowledge concerning related events in similar scenes. This wiki describes how the auditory system might construct the initial representation of an auditory event from the sound waves entering the ear from the environment.
The focus is on communication sounds like those that occur when a performer sings a melody or recites a line of poetry. These sounds are similar in form to the territorial calls of animals. Communication sounds are dominated by complex tones about a quarter of a second in duration. These communication tones are heard as the vowels of speech and the notes of melodies, as well as the hoots and coos in animal calls.
It is argued that these complex tones are the basic building blocks of auditory perception. They produce stable structures with distinctive shapes in the auditory image, and these auditory figures are often sufficient to identify the source of the sound. Sequences of these auditory figures give auditory events meaning and segregate the auditory scene into foreground and background events.
This section of the wiki explains the production of communication sounds, the form of the information in communication sounds, and how the auditory system converts these sounds into the perceptions we hear when they occur in everyday life. It explains what is meant by the terms auditory figure, auditory image, auditory event, the auditory scene, and auditory objects. It also explains how the auditory system might create the internal, neural representations of sound that support auditory perception and bio-acoustic communication. The focus is on signal processing transforms that can be applied to all sounds to produce an internal space of auditory events where the important features of communication sounds are automatically segregated in preparation for subsequent perceptual processing.
The page below provides an introduction to the auditory image. The wiki is still being developed and some of the supporting pages are still under construction.
There are computational versions of AIM written in Matlab and C. They are referred to as AIM-MAT and AIM-C, and they can be obtained from the SoundSoftware repository. There is tutorial that provides a introduction to computational audition.
Contents |
Part 1: Communication Sounds and Acoustic Scale
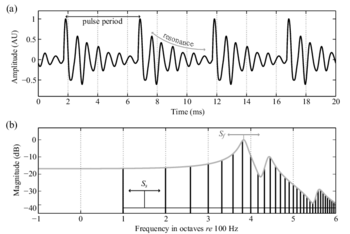
The tones of communication sounds have a special pulse-resonance form (Figure 1.0.1a) that distinguishes them, as a class, from environmental noises like wind in the trees or waves on the beach, and from mechanical noises like those produced by air-conditioning systems or jet aeroplanes. The distinctive pulse-resonance form arises from the way the sounds are produced. Briefly, a source (like the vocal folds) produces a stream of acoustic pulses (the large peaks in Figure 1.0.1a), and then resonators (like the mouth and throat) filter the pulses leaving a characteristic resonance on the back of each pulse. The shape of the resonance in the waveform determines the shape of the envelope of the spectrum of the sound (the grey line in Figure 1.0.1b). In this case, the envelope shape indicates that this tonal sound is a human vowel, which the speech system might recognize as the /ae/ of "hat".
As a child grows up, their vocal folds and their vocal tract (mouth and throat) both increase in size, with the result that the pulse rate and the resonance rate of their sounds both decrease. The acoustic information concerning the size of the source, as it appears in the waveform and the spectrum of the sound, is referred to as the Acoustic Scale of the source, Ss. In the spectrum, it determines the position of the set of harmonics (vertical lines) along the frequency axis when the spectrum is plotted on a logarithmic scale (as in Figure 1.0.1b). The harmonics move as a unit with changes in source size on a log frequency axis. The acoustic information concerning the size of the filter, as it appears in the waveform and the spectrum of the sound, is referred to as the Acoustic Scale of the filter, Sf. In the spectrum it determines the position of the spectral envelope along the frequency axis when the spectrum is plotted on a logarithmic scale.
The envelope shape information conveyed by a short sequence of pulse-resonance tones is sufficient for the auditory system to determine whether a melody is being sung by a human or played by, say, a brass instrument. The acoustic scale values conveyed by a short sequence of pulse-resonance tones are sufficient for the auditory system to determine whether the melody is being sung or played in a high register by a soprano or trumpet, or in a low register by a baritone or French horn.
Part 1 of this wiki describes the form of communication sounds, how they are produced, and how they differ from other categories of sounds such as environmental noises. The focus is on those aspects of communication information that are contained in isolated communication tones, as distinct from those aspects of communication information conveyed by the order of tones in sequences that form melodies or sentences.
Part 2: The Auditory Image and Auditory Figures
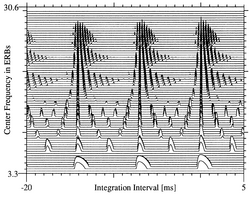
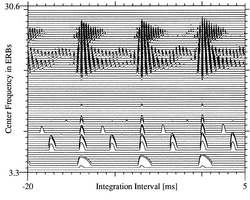
A simulation of the auditory image that might be formed in response to the vowel in “hat” is presented in Figure 2.0.1 to illustrate what is meant by the term "auditory image". The ordinate of Figure 2.1.1 is the “place” dimension of the cochlea which corresponds to the “tonotopic” dimension of auditory perception. The creation of this dimension in the cochlea is described in Chapter 2.2. The abscissa in Figure 2.1.1 is a time-interval dimension rather than a time dimension. In this auditory image space, the repeating pattern of neural activity produced by the cochlea in response to a communication tone appears as a distinctive, stable structure referred to as an auditory figure. The process that creates the time-interval dimension, and thus, the stablized auditory figures, is referred to as 'strobed' temporal integration; it is described in Chapter 2.4. From the physiological perspective, the simulated auditory image is a vertical array of dynamic, time-interval histograms , one for each place along the cochlear partition. The representation provides a relatively simple summary of the information in a communication sound as it appears in the auditory system at the level of the brain stem or thalamus over the most recent 100 ms, or so, of the sound. The auditory image is intended to represent our initial experience of a sound as it occurs in the absence of context, as when a sound comes on unexpectedly.
The auditory figures produced by communication tones contain features that provide important information about the source of the communication. For example, the auditory figure produced by the vowel in "hat" (Figure 2.0.1) tells us five important things about the speaker.
- The vertical ridges of activity above time intervals of 0, 7 and 14 ms show that the period of the vowel is about 7 ms. This is the internal representation of the acoustic scale of the source, Ss. We hear this feature of the auditory image as the pitch of the sound. A period of 8 ms corresponds to a frequency of 125 Hz. The pitch of this vowel is close to the pitch produced by the piano key, B2, just over an octave below middle C on the piano. When the pitch of the voice rises, the ridge moves to the right, and when the pitch falls, it goes to the left.
- The set of rightward pointing triangular shapes hanging on each of the vertical ridges tell us that the source is very likely to be a human. These asymetric triangular features are the hallmark of cavity resonances like those formed by the mouth and throat. These vocal tract resonances are referred to as “formants”.
- The relative positions of the formants indicate that the human is saying, or singing, the vowel, /ae/, at this moment in time. When the vowel type changes the triangles move up and down the vertical ridge. For example, the /i/ vowel in “heat” produces the auditory figure shown in Figure 2.0.2; the first formant has moved down and the second formant has moved up to the point where it encroaches on the region normally occupied by the third formant. For a given individual, the third and fourth formants do not move am much as the first and second formants. The formants of an auditory figure correspond to the peaks in the magnitude spectrum of the sound.
- The vertical position of the auditory figure, indicates that the person speaking is an adult with a relatively long vocal tract. The vertical position of the auditory figure is the internal representation of the acoustic scale of the filter, Sf. If a child with a relatively short vocal tract spoke the same vowel, the auditory figure would have a similar shape but it move up the ordinate an the width of the figure would shrink a little.
- The combination of a relatively low pitch with relatively low formants indicates that the person speaking these two vowels is probably a man, rather than a woman.
These five aspects of communication information are provided by all vowels as properties of the auditory figures that appear in the auditory image. Musical tones and animal calls also produce distinctive auditory figures in the auditory image and the position of the auditory figures along the two dimensions provides information about the size of the instrument or animal producing the tone. Part 2 of the wiki explains how the auditory system might construct the space of auditory images, and it contrasts the structured auditory images produced by communication tones with the featureless auditory images produced in response to noise like wind in the trees.
Part 3: Auditory Events
When a musical tone or a vowel occurs in isolation, we hear it as a simple auditory event with one, fixed, auditory figure containing information about the source of the corresponding acoustic event. The auditory figure comes on abruptly when the acoustic event begins, it remains static for the duration of the acoustic event, and it goes off abruptly when the acoustic event ends. So the simplest auditory events are just auditory figures as they come and go in the auditory image in real time. In the everyday world, the acoustic events of music and speech come in sequences that we hear as compound auditory events and/or sequences of events. We refer to them as melodies, words, phrases etc. The dynamic properties of auditory events are described in Chapter 3.1.
In compound auditory events, the auditory figures that structure the information sometimes change abruptly from one to the next, and sometimes morph gradually from one to the next. The gross dynamic properties of auditory events are dictated by the sound itself in the sense that the sound determines when an auditory figure will appear and disappear in time. However, it is the "strobed" temporal integration mechanism that determines the details of the onset and offset of a figure and whether the figures change from one to another abruptly or gradually. A set of three videos (below) illustrates the form of three compound auditory events and introduces the dynamics of auditory perception. The important thing to note is that the action in the video occurs at the same rate as change takes place in the sound that you hear. [Note: If the motion you see in the videos lags the changes you hear in the sound, try downloading the video to your own machine and playing it there. But be careful; some of the examples are pretty big.]
- The first example is an arpeggio Do-Mi-So-Do . There are continuous glides between the tones. Note that the visual figure in the visual representation of the auditory image morphs smoothly from note to note as the sound glides smoothly from note to note. During each tone the auditory figure is static.
- The second example is a simple Up-Down Melody. There is very little time between the tones in the sound and the auditory figure bounces right and left in discrete steps as the melody proceeds. The example shows that the temporal integration mechanism can stabilize the neural pattern and change abruptly from one note to the next, much as we hear stable notes changing rapidly from one to the next.
- The third example is the word Leo. It shows how the first formant in the /l/ at the start of the word moves up to crowd the second formant during the /i/ of the word and then back down to a middle position during the /o/ of the word.
The videos of auditory events illustrate one of the basic tenants of AIM; the internal, neural representation of sound, associated with the emergence of the concious perception of the sound, is an auditory image in which auditory figures are static when the perception we hear is static and they morph from one figure to another as the perception glides from one static perception to another. Chapter 2.4 of the wiki explains how the temporal integration mechanism in AIM converts temporal information on the physiological time scale (hundreds of microseconds) into the position information that defines an auditory figure. At the same time, the mechanism preserves temporal information on the psychological time scale (hundreds of milliseconds) which we hear as the dynamic changes that define an auditory event. It is this strobed temporal integration mechanism that explains why we perceive the glides between notes in the arpeggio, Do-Mi-So-Do, and why we hear the second formant gliding from /l/ to /i/ to /o/ in "'Leo"'. The rate of cycles in these sounds is on the order of 100 per second. This is high relative to the half life of the integration mechanism (30 ms), so new copies of the auditory figure are entering the image faster than the time taken for the image to decay to half its height. When the sound is periodic successive copies of the figure are the same and strobed temporal integration produces a static auditory figure. When the sound is changing slowly between cycles, successive figures are similar but slightly different with the result that the auditory figure morphs smoothly from one form to the next, much as cartoon characters can be made to morph from one to another.
It is not possible to create a real-time display of an auditory event with both a tonotopic dimension and a time-interval dimension from the traditional representation of sound, the spectrogram. The temporal fine structure that defines the auditory figure is integrated out during the production of the spectrogram. The implication is that spectrographic models are unlikely to provide an intuitive explanation of the subtilties we hear in speech and musical sounds.
Part 4: The Size-Covariant Auditory Image
Part 1 of the wiki explained how the physical size of a singer or instrument affects the acoustic scale of the sounds produced by that singer or instrument, and it explained that there are two aspects to the size information; there is the size of the excitation mechanism that produces the pulses and the size of the filters in the body of the singer or instrument that produce the resonances. Parts 2 and 3 of the wiki illustrated the form that communication information takes in the internal representation of sound, that is, in auditory images, auditory figures and auditory events.
Part 4 of the wiki begins by drawing attention to something everyone instinctively knows; listeners can understand what speakers are saying independent of speaker size (man, woman or child). In signal processing terms, auditory perception is exceptionally robust to changes in the acoustic scale values of a communication sound. The supporting chapters present a series of behavioural experiments designed to document listeners' ability to (1) extract the message of the communication independent of the size of the speaker, and (2) extract the size information in the sound independent of the message of the communication.
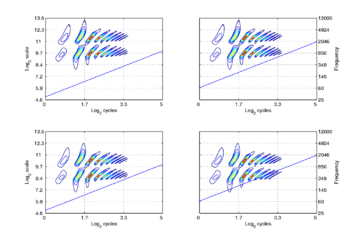
The experiments suggest that the internal, auditory representation of sound is automatically normalized to produce a scale-invariant, or scale-covariant, representation of the information in communication sounds (Irino and Patterson, 2002; Patterson et al., 2007). The remainder of Part 4 explains how to convert the "linear time-interval" dimension of the auditory image (as illustrated in Parts 2 and 3) into a "log-cyles" dimension that makes the auditory image scale-shift covariant. [The scale-invariant representation of the auditory image is the Mellin Image decribed in Irino and Patterson (2002)].
In the scale-shift covariant auditory image, the information of the auditory figure appears superimposed of a set of vertical ridges that represent the impulse response of the auditory filterbank. The pulse rate appears as a diagonal in this normalized auditory image. When the pulse rate increases or decreases, the diagonal moves up or down without changing the shape or position of the normalized auditory figure. As the size of the resonances in the body of the speaker or instrument increase, the position of the auditory figure moves down without changing shape, and it does so independent of the diagonal the shows the pulse rate. The following examples illustrated the separation of the three forms of information in the covariant auditory image.
- The first example is the arpeggio Do-Mi-So-Do but now the auditory image has the covariant form. There are continuous glides between the tones. The instrument is a simple click train produced by a computer so there is no sculpting of the filterbank impulse response in this case. The only thing that is changing in this example is the pulse rate of the sound, and the only motion in the image involves the position of the diagonal; its position is fixed during the notes Do, Mi, So and Do and it moves up during the glides between the notes.
- The second example is the Up-Down Melody with the auditory image in covariant form. The only thing that is changing in this example is the pulse rate of the sound, and the only motion in the image involves the position of the diagonal which moves up in discrete steps and then down in discrete steps as the melody proceeds.
- The third example is the word Leo with the auditory image in covariant form. The formants of the vocal tract sculpt the impulse response of the auditory filterbank. The example shows how the first formant in the /l/ at the start of the word moves up to crowd the second formant during the /i/ of the word and then back down to a middle position during the /o/ of the word. The word is spoken in a monotone voice and so the diagonal is essentially fixed as the formants move up and down the impulse response.
[Note: If the motion you see in the videos lags the changes you hear in the sound, try downloading the video to your own machine and playing it there. But be careful; some of the examples are pretty big.]
The following syllable pairs illustrate how the message of a syllable (whether it is /da/, /mu/ or /ke/) is segregated from the information about the scale of the source (i.e. glottal pulse rate) and the scale of the filter (i.e. vocal tract length) in the covariant auditory image. A natural /da/ syllable spoken by a man on a low pitch is compared with syllables in which
- the message changes from /da/ to /de/, holding glottal pulse rate and vocal tract length fixed, or
- the glottal pulse rate changes from 137 to 183 Hz, holding syllable type and vocal tract length fixed, or
- the vocal tract length changes from 15.7 to 10.5 cm, holding syllable type and glottal pulse rate fixed.
Part 5: Auditory Objects and the Auditory Scene
Part 5 of the wiki is concerned with what is meant by "auditory objects." It is argued that we should distinguish "auditory objects" from "auditory figures", "auditory events", "auditory images" and "auditory scenes," and establish what we mean by each of these terms. The basic problem is to relate the external world of objects to the visual and auditory representations of these objects as they occur in the brain. It is assumed that:
- A Visual Object is the visual part of your experience of an external object, or event, including visual knowledge associated with the object, and by analogy,
- An Auditory Object is the auditory part of your experience of an external, acoustic event involving an object, including auditory knowledge associated with the object.
So, for example, you can think of a word like "leo" as an auditory object. It is an auditory event with meaning, as distinct from the sequence of auditory figures that defines the auditory event that causes the brain to search out the meaning that goes with this auditory event and attach it to the event to produce our experience of the word, which is the auditory object.
There is an introductory chapter that describes the concepts and develops terminology to distinguish the acoustic properties of sound from the corresponding properties as they arise in the internal, auditory representations of sounds as they occur in the brain. Imagine the situation in which an animal that we have never encountered before emits its territorial call. We do not have any knowledge concerning the call. Nevertheless, the sound elicits a sequence of largely data-driven processes that covert this coherent segment of sound, which we might think of as an acoustic event, into a dynamic, coherent internal representation that we experience as an auditory event. The concepts and their relationships might be described in the following terminology:
![I_A \bigl[ E_A \bigl\{ F_A^n(s_a) \bigr\} \bigr]
\quad\xleftarrow{\quad A \quad}\quad
s \bigl[ e_a \bigl\{ p_e^n \bigl( s_a \bigr) \bigr\} \bigr]](../images/math/d/a/2/da2eb15b0e7192f81610ec0f61592185.png)
In words, the right-hand side of the equation, which deals with the external world, says:
The acoustic scene, ![s [\ \cdot\ ]](../images/math/a/2/9/a29a9680df1d386d5bbf1b140c9f50c2.png) , contains an acoustic event,
, contains an acoustic event, 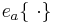 , which is a sequence of pulses (with their resonances),
, which is a sequence of pulses (with their resonances), 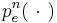 , emitted by an acoustic source, sa, in an external object. The auditory system converts the external scene,
, emitted by an acoustic source, sa, in an external object. The auditory system converts the external scene, 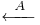 , into an auditory image,
, into an auditory image, ![I_A [\ \cdot\ ]](../images/math/d/9/1/d9112a87aa40dcbd7b5590e4d2cb603c.png) , which contains an auditory event,
, which contains an auditory event, ![E_A [\ \cdot\ ]](../images/math/1/8/c/18c0e18cc8a0246e83ff323be3aac24b.png) , which is a sequence of auditory figures,
, which is a sequence of auditory figures, ![F_A^n [\ \cdot\ ]](../images/math/8/f/6/8f66638c4a06b63077de4e8b74712215.png) , one for each pulse-resonance cycle emitted by the acoustic source, sa. (External concepts are denoted with lower case letters and internal auditory concepts by upper case letters.)
, one for each pulse-resonance cycle emitted by the acoustic source, sa. (External concepts are denoted with lower case letters and internal auditory concepts by upper case letters.)
Once the terminology for specifying concepts in the external and internal worlds is set out, the chapter extends the terminology to include meaning and auditory objects. The discussion begins with Rene Magritte's famous painting "This is not a pipe." The "pipe" in the figure is not a real pipe. It is a painting of a pipe with an inscription that is intended to prompt discussion about art and illusion. The discussion then turns to an auditory analogy of Magritte's painting -- a video showing the activity that arises in the auditory image as a person speaks the sentence "Ceci n’est pas le mot pipe." It is clear that the video presents a sequence of auditory events corresponding to a sequence of acoustic events. The question is whether the auditory event produced by the sound /pip/ is an auditory object, since the brain automatically attaches a very specific meaning to the event?
Loading the player... Download CeciNestPasLeMotPipe.mov [7.47 MB] |
Part 6: Auditory Image Research
The primary hypothesis of the Auditory Image Model (AIM) is that the auditory system converts all sounds into scale-shift covariant auditory images (cvAIs), which the auditory brain then combines with contextual information to construct our experience of acoustic events in the world (Patterson et al., 1992; Patterson, 1994). AIM is very specific about the data-driven processes that construct the initial auditory image of a sound and this has led to several strands of research designed to (i) test the underlying hypotheses in AIM, (ii) delimit the parameters values of the model, or (iii) identify regions of the brain beyond the cochlea where different aspects of the processing might be located. Part 6 provides an introduction to some of the current strands of research.
The perception of family and register in musical tones
A chapter has been written to explain the role of acoustic scale in the perception of instrument register (Patterson et al., 2010). It describes how four families of orchestral instruments produce their sounds in source-filter terms (Section 3), and how the auditory system extracts the acoustic scale information from musical tones and combines the scale values, Ss and Sf, to produce the perception of instrument register within a family (Section 4). The discussion suggests (Section 5) that we might want to revise the definition of timbre to incorporate the acoustic distinction between envelope shape and envelope position (i.e. Sf), and distinguish between family timbre, which is based mainly on envelope shape, and register timbre, which is based mainly on acoustic scale (a combination of Ss and Sf). The discussion is current being extended to the perception of register within a given instrument, to determin the extent to which the Ss/Sf ratio explains distinctions made between the perception of the upper and lower register within an instrument's range.
- Introduction
- Pulse-resonance sounds and acoustic scale
- The pulse-resonance tones of musical instruments
- The auditory representation of pulse-resonance sounds and acoustic scale
- The acoustic properties of pulse-resonance sounds and the auditory variables of perception
- Conclusions
The distortion produced by compression in the cochlea
Lyon (2010) has recently described how a cascade of simple asymmetric resonators (CAR) can be used to simulate the filtering of the passive basilar membrane, and how the parameters of a CAR can be manipulated with an integral AGC network to simulate the fast-acting compression (FAC) that characterizes the spectral analysis performed in the cochlea. Walters (2011) has recently implemented a version of Lyon’s CAR-FAC as a filterbank option in AIM, both in AIM-C, the real-time version of AIM, and AIM-MAT, the MATLAB version of AIM with a GUI for teaching and model development.
The cascade architecture of CAR-FAC systems means that the distortion generated by compression in one channel of the cascade propagates down through the channels to the one with the appropriate centre frequency. This suggests that the CAR-FAC module in AIM-C might enable us to study the role of compressive distortion in the perception of complex sounds like speech and music. The sections below describe the proposed research as it is currently envisaged.
- CAR-FAC systems and compressive distortion
- Perceptual evidence of compressive distortion: direct measures
- Perceptual evidence of compressive distortion: indirect measures
- When is distortion perceived as DIstortion ?
- The traditional description of distortion
The space of auditory perception
AIM makes very specific predictions about the space of auditory perception and the internal representations of sound in the auditory pathway. Sound, with dimensions {amplitude and time}, is converted into an auditory image with dimensions {compressed-amplitude, time, log-scale, and log-cycles}. The extra dimensions are constructed in two relatively straightforward stages:
- The log-scale dimension is introduced by the compressive wavelet analysis performed in the cochlea. The output is a Neural Activity Pattern (NAP) with dimensions {compressed-amplitude, time, and log-scale}.
- The log-cycles dimension is introduced by strobed temporal integration which cuts the NAP into segments on amplitude peaks and combines the segments in an image buffer with a 30-ms half life. This process separates the temporal microstructure of the NAP from the slower, envelope modulations associated with the dynamics of acoustic events. The temporal microstructure of the NAP appears as spatial information across the log-cycles dimension of the auditory image. The envelope information of the NAP appears in the dynamics of the auditory figure which defines psychological time in auditory perception.
A detailed description of the scale-shift covariant auditory image is provided by Patterson et al. (2007). It includes a unitary operator that defines the covariant space mathematically. A detailed description of the scale-shift invariant Mellin Image is provide in Irino and Patterson (2002). Note, however, that the mathematics is linear and does not explain how compression operates within auditory image space. One of the computational versions of AIM referred to as AIM-C includes a cascade filterbank with fast acting compression which may make it possible to simulate compressive distortion in auditory image space.
Size Matters! The wavelength view of register information
The instruments of the orchestra come in families (e.g. the string family, the brass family, the woodwinds and the family of human voices). Within a family, the members are distinguished by their register which in the case of the violin family runs from the high register of the violin through to the low register of the contra bass. In all families of musical tones, register is larely determined by the size of the instrument -- the size of the pulse generating components like the strings, and the size of the resonant components of the instrument body. This paper considers the form of the size information in terms of the properties that represent the register information in four domains from production in the instrument to perception in the brain. The properties and domains are:
- the physical properties of the sound generating components of the instrument,
- the acoustic properties of the sound as it exists in the air,
- the physiological properties of the internal auditory representation of sound, and
- the perceptual properties of the music we hear.
The description focuses on wavelength rather than frequency because wavelength bears a direct rather than inverse relationship to size, and thus register in all four domains.
Acknowledgements
The acoustic scale wiki was set up by Tom Walters and Etienne Gaudrain at the CNBH in PDN at the University of Cambridge. At that time, Tom Walters was supported by a grant from AFOSR through EOARD, and Etienne Gaurdrain was supported by a grant from the UK MRC (G9900369). Much of the content of the wiki was loaded by the scientists who performed the research.
References
- Irino, T. and Patterson, R.D. (2002). “Segregating Information about the Size and Shape of the Vocal Tract using a Time-Domain Auditory Model: The Stabilised Wavelet-Mellin Transform.” Speech Commun., 36, p.181-203. [1] [2] [3]
- Patterson, R.D. (1994). “The sound of a sinusoid: Time-interval models.” J. Acoust. Soc. Am., 96, p.1419-1428. [1]
- Patterson, R.D., Gaudrain, E. and Walters, T.C. (2010). “The Perception of Family and Register in Musical Tones”, in Music Perception, Jones, M.R., Fay, R.R. and Popper, A.N. editors, p.13-50 (Springer-Verlag, New York). [1]
- Patterson, R.D., Robinson, K., Holdsworth, J., McKeown, D., Zhang, C. and Allerhand, M. (1992). “Complex Sounds and Auditory Images”, in Auditory Physiology and Perception, Y Cazals L. Demany and Horner, K. editors (Pergamon Press, Oxford). [1]
- Patterson, R.D., van Dinther, R. and Irino, T. (2007). “The robustness of bio-acoustic communication and the role of normalization”, in Proceedings of the 19th International Congress on Acoustics, p.07-011. [1] [2]
Pages in category "Auditory Image"
The following 56 pages are in this category, out of 56 total.