The processing and perception of size information in speech sounds
From CNBH Acoustic Scale Wiki
There is information in speech sounds about the length of the vocal tract; specifically, as a child grows, the resonators in the vocal tract grow and the formant frequencies of the vowels decrease. It has been hypothesized that the auditory system applies a scale transform to all sounds to segregate size information from resonator shape information, and thereby enhance both size perception and speech recognition [Irino and Patterson, Speech Communication 36, 181-203 (2002)]. This paper describes size discrimination experiments and vowel recognition experiments designed to provide evidence for an auditory scaling mechanism. Vowels were scaled to represent people with vocal tracts much longer and shorter than normal, and with pitches much higher and lower than normal. The results of the discrimination experiments show that listeners can make fine judgements about the relative size of speakers, and they can do so for vowels scaled well beyond the normal range. Similarly, the recognition experiments show good performance for vowels in the normal range, and for vowels scaled well beyond the normal range of experience. Together, the experiments support the hypothesis that the auditory system automatically normalizes for the size information in communication sounds.
David Smith , Roy Patterson
Contents |
Introduction
Most animals generate their communication sounds by exciting resonant cavities in the body with a stream of sharp acoustic pulses. The resonators grow as the animal grows, and as a result, the calls of animals contain information about the size of the individual. Behavioural studies show that, when animals vocalize to attract or repel suitors, or to establish and defend territories, the size of the sender is an important part of the communication. The effect of size has been documented for many species: for example, frogs (Fairhall, 1981, Narins and Smith, 1986), dogs (Riede and Fitch, 1999), deer (Clutton-Brock and Albon, 1979) and monkeys (Fitch, 1997). Cohen (1993) has argued that size is a dimension of sound much like frequency and time, and he has developed a version of the affine Mellin transform (Titchmarsh, 1948) that can segregate the size information in a sound from the size-invariant information. The implication is that animals have evolved a physiological form of this Mellin transform which operates at a relatively early point in the auditory system, and that this is the basis of the size processing observed in animal behaviour. The purpose of the current paper was to investigate the perception of size information in speech sounds to see if it is compatible with the hypothesis that the auditory system applies a size-normalizing transform to all sounds prior to the commencement of speech specific processing. The physiological mechanism that humans use to produce speech sounds is the same as that used by all mammals to produce their calls; the vocal cords in the larynx produce glottal pulses which excite resonances in the vocal tract beyond the larynx. As a child grows into an adult, there is an increase in vocal tract length (VTL) (Fitch and Giedd, 1999), and as a result, the formant frequencies of the vowels decrease (Fant, 1960; Fitch and Giedd, 1999; Huber, Stathopoulos, Curione, Ash and Johnson, 1999), and this is an important form of size information in speech. A second source of size information is glottal pulse rate (GPR) measured in Hz. GPR is determined largely by the length and mass of the vocal folds (Titze, 1989), both of which increase with sex and age. In males, at puberty, there is an additional spurt in VTL and a sudden drop in GPR which complicates the interpretation of VTL and GPR information with respect to speaker size. This is an important issue but it is not the topic of this paper and care is taken in the design of the experiments to avoid complications associated with speaker sex and the abrupt changes that occur at puberty in males. Irino and Patterson (1997, 1999a,b,c, 2002) have developed a two-dimensional, pitch-synchronous version of the Mellin transform to simulate the processing of size information in speech. They have shown that the transform can segregate VTL information from information about vocal tract shape (vowel type). It is assumed that the VTL information is used to evaluate speaker size, and that the normalized shape information facilitates vowel recognition. Both Turner et al. (2004) and Welling and Ney (2002) have demonstrated the advantage of normalization in machine recognition of vowels sounds. This paper focuses on the two complimentary aspects of size processing: a) the ability to discriminate a change in the size of the speaker, and b) the ability to normalize across size differences in order to extract the size-invariant properties of vowels (i.e., vowel type).
Speaker size discrimination
If size functions as a dimension of sound for humans, then we might expect to find that listeners can readily make fine discriminations about speaker size just as they can for loudness or brightness. Moreover, if it is a general mechanism, we should expect to find that they make size judgments even when the vowel sounds are scaled to simulate humans much larger and smaller than those normally encountered. Kawahara, Masuda-Kasuse and de Cheveigne (1999) have recently developed a high-quality vocoder, referred to as STRAIGHT, that uses the classical source-filter theory of speech Dudley (1939) to segregate GPR information from the spectral-envelope information associated with the shape and length of the vocal tract. Liu and Kewley-Port (2004) have reviewed STRAIGHT and commented favourably on its ability to manipulate formant related information. STRAIGHT produces a pitch-independent spectral envelope that accurately tracks the motion of the vocal tract throughout the utterance. Subsequently, the utterance can be resynthesized with arbitrary changes in GPR and VTL; so for example, the utterance of a man can be readily transformed to sound like a women or a child (Kawahara, 2003; Kawahara and Matsui, 2003). The utterance can also be scaled well beyond the normal range of GPR and VTL values encountered in everyday speech. We used STRAIGHT to scale vowels which could then be used to measure size discrimination, that is, the smallest change in VTL required to reliably discriminate a change in speaker size. The experiments were performed both within the normal range of the human voice and in a much larger region of the GPR-VTL space surrounding that range.
Vowel normalization
If the size processing hypothesis is correct, then it is likely that vowel normalization is a natural by-product of size processing. Vowel normalization refers to the fact that humans readily recognize that the sounds produced by men, women and children saying a given vowel, such as /e/, are indeed the same vowel, despite gross differences in the waveforms. If size processing is applied to all sounds at a relatively early stage in auditory processing, and if it is the basis of vowel normalization, then we should find that vowel recognition, like size discrimination, is largely immune to the scaling of vowel sounds beyond the normal speech range. Assmann et al. (2002, 2003) have recently measured vowel recognition within the normal speech range and somewhat beyond in humans, using vowels scaled by STRAIGHT. They argue that the auditory system employs a form of neural net to learn which formant frequencies (spectra) go with which vowel type, and that it learns the connections for all values of GPR in the normal speech range. They interpret the deterioration in recognition performance for their more extreme stimuli as evidence of the neural net failing to generalize beyond the training set. But they do not consider the possibility of a general purpose size mechanism as suggested by Cohen (1993) or Irino and Patterson (1999a,b,c). The experiments of Assmann and colleagues are limited to GPRs in the normal speech range and above it. In this paper, we report complimentary experiments in which vowel recognition is measured in the normal speech range and for vowels in a three-octave range below that which is normally experienced. In the discussion, we compare the results from the two sets of studies and evaluate the relative merits of “general-purpose normalization” and the “neural net” hypothesis as explanations of the observed recognition performance.
Method
Stimuli
We recorded the English vowels (/a/, /e/, /i/, /o/, /u/) as spoken by author RP in natural /hVd/ sequences (i.e., haad, hayed, heed, hoed, who’d) using a high quality microphone (Shure SM58-LCE) and a 44.1-kHz sampling rate. The vowels were sustained (e.g., haaaad) and the natural onset of the vowel was preserved whilst avoiding the aspiration of the preceding /h/. A cosine-squared amplitude function was used to gate the vowels on over 5 ms and off over 30 ms. The central plateau was 565 ms, so the total duration of each vowel was 600 ms. The vowels were normalised to the same RMS level (0.1, relative to maximum ±1). The pitch of the vowels was scaled to 113 Hz which is near to the average for men. These five vowels comprise what is referred to as the “canonical” vowels. The scaling of the vowels was performed using STRAIGHT (Kawahara et al., 1999). It is referred to as a vocoder (voice coder) but it is actually a sophisticated speech processing package that dissects and analyses an utterance with glottal cycle resolution. It produces a pitch-independent spectral envelope that represents the vocal tract information independent of glottal pulse sampling. Vocal tract shape determines which vowel type is encoded by the shape of the spectral envelope; vocal tract length determines the scale of the pattern, and this is the form of the VTL information. Once STRAIGHT has segregated a vowel into glottal pulse rate and spectral envelope frames, the vowel can be resynthesized with the spectral-envelope dimension (frequency) expanded or contracted, and the glottal-pulse-rate dimension (time) expanded or contracted, and the operations are largely independent. Utterances recorded from a man can be transformed to sound like a women or a child; examples are provided on our web page1. The distinctive advantage of STRAIGHT is that the spectral envelope of the speech that carries the vocal tract information is smoothed as it is extracted, to remove the harmonic structure associated with the original GPR, and the instantaneous zeros produced by the interaction of GPR and the frame rate of the analysis window. As a result, the resynthesized utterances are of extremely high quality even when the speech is resynthesized with GPR and VTL values well beyond the normal range of human speech (provided the GPR is not far above the first formant). The scaling of GPR is simply a matter of expanding or contracting the time axis of the sequence of glottal events. The scaling of VTL is accomplished by compressing or expanding the spectral envelope of the speech linearly along a linear frequency axis. On a logarithmic frequency axis, the spectral envelope shifts along the axis as a unit. The change in VTL is described by the spectral envelope ratio (SER), that is, the ratio of the unit on the new frequency axis to that of the axis associated with the original recording. Note that values of SER less than unity indicate lengthening of the vocal tract to simulate larger men, and SERs greater than unity indicate shortening of the vocal tract to simulate smaller men, women and children. Following the scaling of GPR and VTL by STRAIGHT, the first 100 ms of the wave was removed because the abruptness of the original gate caused STRAIGHT to overshoot at onset. Then, a cosine-squared gating function (10-ms onset, 30-ms offset, 465-ms plateau) was used to select a stationary part of the vowel. The RMS level was set to 0.025 (relative to maximum ±1). The stimuli were played by a 24-bit sound card (Audigy 2, Sound Blaster) through a TDT anti-aliasing filter with a sharp cutoff at 10 kHz and a final attenuator. The stimuli were presented binaurally to the listener over AKG K240DF headphones. Listeners were seated in a double-walled, IAC, sound-attenuating booth. The sound level of the vowels was 66 dB SPL.
Procedures and listeners
Discrimination procedures
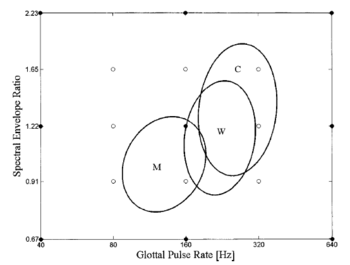
The just noticeable difference (JND) in speaker size was measured in two discrimination experiments. One measured discrimination performance using single vowels and the other used a more speech-like sequence of four vowels. The two paradigms are referred to as the single-vowel and speech-like discrimination tasks. Both discrimination experiments employed a two interval, two-alternative, forced-choice paradigm (2AFC) with the method of constant stimuli. One interval contained the standard stimulus, the other contained the test stimulus in which the simulated VTL of the speaker was either larger or smaller. The order of the test and standard intervals in each trial was chosen randomly and the listener's task was to choose the interval in which the vowel(s) were spoken by the smaller speaker. The listeners were given written instructions explaining the task in terms of speaker size. Most listeners considered it a natural task to judge the size of speaker of the vowel sounds. One listener initially maintained that the task would be too difficult but was in fact easily able to do the task by “thinking of the speakers as cartoon characters”. No feedback was given in either experiment. In the first discrimination experiment, the two temporal intervals of a trial each contained a single vowel of the same type (i.e., /a/ was compared with /a/). The listener was required to choose the interval in which the vowel was spoken by the smaller speaker. Psychometric functions for VTL discrimination were gathered with this single-vowel paradigm at nine widely spaced points on the GPR-SER plane – the combinations formed by three GPRs (40, 160 and 640 Hz) and three SERs (0.67, 1.22 and 2.23) cf. Fig. 1. At each of the nine GPR-SER points, a psychometric function was measured with six test SER (VTL) values bracketing the standard SER (VTL) value. A psychometric function was collected for each of the five vowels. The psychometric functions around one GPR-SER standard point were collected in one run (taking 30 min per listener), and consisted of ten blocks of 30 trials, where each block contained the six tests from the five vowels. Each listener thus provided 60 trials per psychometric function for each of the five vowels.
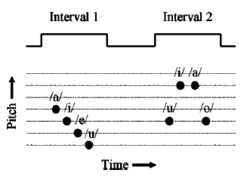
By its nature, a change in vocal tract length produces a shift of the vowel spectrum along the frequency axis, and so it might be possible for a listener to focus on one formant peak and perform the task by noting whether the peak shifts up or down in the second interval. It is our impression that this was not what the listeners did, and that it would be difficult, if not impossible, to do. Nevertheless, it is a logical possibility, and so, in a second discrimination experiment, we used a more speech-like paradigm, which effectively precluded the possibility of using a simple spectral cue. The paradigm is presented in quasi-musical notation in Fig. 2. Each temporal interval of the 2AFC trial contained a sequence of four of the five vowels chosen randomly without replacement, and the vowels were presented with one of four pitch contours (rising, falling, up-across-down, down-across-up). The duration of the vowels was 400 ms (15-ms onset, 90-ms offset), and each interval gave the impression of a person carefully pronouncing a sequence of vowels at a reasonably natural rate (four vowels in 1.6 s). The pitch values were drawn from an equal-temperament, quarter-tone musical scale, in which the pitch of each note differed from its neighbours by just under 3%. The starting point for the pitch contour was varied randomly over a 9% range, and the level of the vowels in a given interval was roved in intensity over a 6 dB range. The only fixed parameter within an interval was simulated speaker VTL, and the only consistent change between intervals was speaker VTL. The listeners’ task was to choose the interval in which the vowels were spoken by the smaller speaker, independent of the pattern or pitch or loudness of the vowels. In this paradigm, the listener cannot do the task by choosing a single spectral component in one vowel and noting whether it goes up or down when the same vowel occurs in the second interval. For each combination of SER and GPR, a six-point psychometric function was measured with ten trials per point per listener. A total of 17 psychometric functions were gathered at widely spaced points on the GPR-SER plane (cf. Fig. 1). Perceptually, this paradigm prompts the listener to think of the sounds in the two intervals as coming from two different speakers; the natural prosody of the sequences discourages listening for spectral peaks. The steps in the pitch contours were limited to quarter tones because larger steps made the sequences less speech like. Randomizing the starting point of the contour precludes the possibility of tracking a single harmonic in one vowel from the first interval to the second. The level was not varied within interval because it made the sequences less speech like. The fixed level difference between intervals reinforced the impression that the speakers in the two intervals were different. For comparison, pitch discrimination was measured for five of the nine GPR-SER combinations, using the same paradigm as used to measure VTL discrimination for single vowels. In this case, the VTL of the vowels was fixed and the pitch was varied between intervals. The listener had to choose the interval containing the vowel with the higher pitch. Psychometric functions for pitch discrimination were collected at the center of the normal range (160 Hz, 1.22 SER), and the four extreme discrimination points with GPRs of 40 and 640 Hz, and SERs of 0.67 and 2.23 (cf. Fig. 1).
Recognition procedures
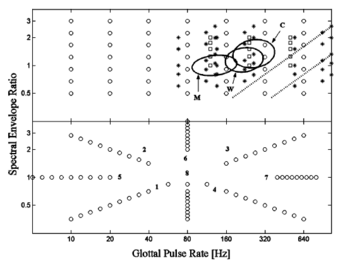
The “surface” paradigm involved a rectangular grid with all 49 combinations of 7 GPR and 7 SER values as shown in the upper panel of Fig. 3 (large open circles); it was designed to measure the surface of recognition performance over a wide range of GPR and SER values to reveal where performance begins to deteriorate. The GPR values ranged from 10 to 640 Hz in doublings; that is from more than an octave below the lower limit of periodicity pitch (32 Hz, Pressnitzer et al., 2001), to about an octave above the pitch of young children. The SER values ranged from 0.5 to 3.0 in seven equal steps on a logarithmic scale; that is, the longest of the simulated vocal tracts was about 32 cm and the shortest was about 5 cm2. If we extrapolate from the known relationship between VTL and body height, VTLs of 32 and 5 cm correspond, respectively, to a man 14 feet tall and newborn baby (1 foot long). Each run contained one trial of all conditions for each vowel (a total of 7 GPRs x 7 SERs x 5 vowels, or 245 trials). Each listener contributed ten runs to the surface map of vowel identification. The listeners were reminded of the five canonical vowels at the start of the run, and at 100-trial intervals thereafter. Each run took approximately 15 min to complete. No feedback was given during data collection. The “strip” paradigm was intended to provide detailed information about the deterioration in performance along 8 spokes radiating from the center of the recognition surface; the specific combinations of GPR and SER for each strip are shown in Fig. 3 (lower panel). Each strip consisted of nine combinations of GPR and SER, making a total of 9 (sample points) x 5 (vowels) x 10 (repetitions), or 450 trials per strip. For three of the listeners in strips 1, 8 and 4 an extra (easier) point was added to ensure that these listeners’ correct recognition scores approached 100%. The stimuli were presented in pseudo-random order in blocks of 45 trials (9 sample points x 5 vowels), and the 10 replications were presented sequentially within a session. Each strip took approximately 30 minutes to complete. As a reminder of the mapping of vowel sound to button, the five canonical vowels were presented with feedback at the start of each run and thereafter at 100-trial intervals. The order of the eight runs required to gather the data for the eight strips was varied between listeners to balance the effects of experience and/or fatigue. No feedback was given during data collection.
Limit on the GPR/F1 ratio
There is a limitation on the GPR that can be used when producing vowels with long vocal tracts. As GPR increases, the fundamental, F0, eventually becomes greater than the frequency of the first format, F1, and as this happens, the first formant becomes very weak relative to the higher formants and the distinctiveness of the vowel deteriorates. The limitation is illustrated for the vowel /e/ by the dotted diagonal lines in the lower right-hand corner of Fig. 3 (upper panel). The upper dotted line shows the combinations of GPR and SER where F0 coincides with F1 (GPR/F1 = 1); the lower dotted line shows the combinations of GPR and SER where F0 coincides with 2F1 (GPR/F1 = 2). As the GPR/F1 ratio increases across the region between the dotted lines towards higher GPRs or smaller SERs (longer vocal tracts), the distinctiveness of the vowel deteriorates, although the stimulus still sounds vowel-like. Thus, normalization is still applied to these sounds, but the perceptual information used to specify the vowel type gradually fades out of the representation. For the vowels /i/ and /u/, the corresponding dotted lines would be a little higher because F1 is lower in these vowels; for the vowels /o/ and /a/, the corresponding dotted lines would be a little lower because F1 is higher in these vowels. Since the limitation varies with vowel type, and the level of F1 decreases continuously in the region of the GPR/F1 limit, discrimination of speaker size and vowel recognition would be expected to deteriorate gradually across this region rather than abruptly. Note, however, that the normal range of vowels (the ellipses) is not far above the upper dotted line, particularly for women and children, and the limitation is highly asymmetric. That is, there is no corresponding limitation to vowel production on the other side of the normal speech range. We will return to this limitation in the Results and Discussion.
Listeners
The recognition experiments were performed before the discrimination experiments. There were five listeners in each of the four experiments. Two listeners participated in all the experiments. Another two listeners took part in all the experiments except the speech-like discrimination task; they had left Cambridge by the time this experiment was designed. So, one new listener was recruited to participate in the single-vowel discrimination experiment only, to make a total of five listeners for that experiment. Then, three new listeners were recruited to participate in the speech-like discrimination experiment. The listeners ranged in age from 20 to 52 years, and were paid student volunteers. All had normal absolute thresholds at 0.5, 1, 2, 4 and 8 kHz. One listener was an author (DS); all other listeners were naïve to the purpose of the experiments.
Results
The results show that detecting a change in speaker size based on a change in VTL (SER) is a relatively easy task for a wide range of VTLs. Performance remains above threshold for a range of GPR and SER values far exceeding those associated with everyday speech. Similarly, vowel recognition performance remains above threshold for a range of GPR and SER values far greater than the normal speech range. The results are presented briefly in this section and interpreted with respect to the underlying mechanisms in the Discussion. In both the discrimination and recognition experiments, the pattern of results was similar across listeners and the levels of performance were comparable, and so, the results will be presented in terms of the average over the five listeners in all cases.
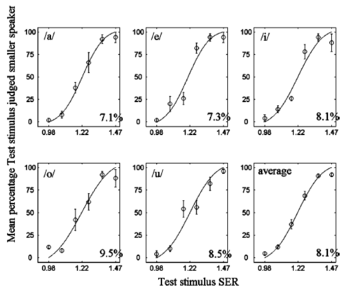
Discrimination of VTL and GPR
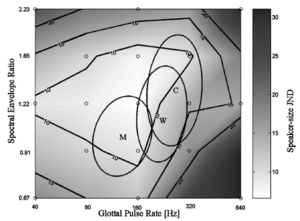
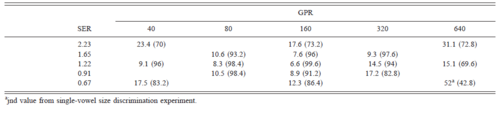
Listeners naturally hear changes in VTL as changes in speaker size. The JND for speaker size was initially measured using the single-vowel discrimination paradigm at nine points in the GPR-SER plane (Fig. 1). The psychometric functions for size discrimination in the center of the normal range (160 Hz, 1.22 SER) are presented separately for the five different vowels and their average (Fig. 4). The mean percentage of trials on which the test stimulus was judged to be spoken by the smaller speaker is shown as a function of the SER of the test stimulus. The group psychometric functions are similar for all vowels; they are monotonic and have relatively steep slopes, confirming that performance is similar across listeners. Cumulative Gaussian functions were fitted to the psychometric functions (Foster and Bischof, 1997). The SER value at the mid-point of the function (50%) is referred to as the point of subjective equality; it was typically within 1% of the standard used to generate the psychometric function which indicates that the perception of speaker size (SER or VTL) was unbiased. The JND was defined as the difference in SER between the values associated with 50 and 76 percent correct (d’=1 in this 2AFC task) relative to the perceived SER (50 percent correct) of the standard, expressed as a percentage. The average JND was 8.1% (with a standard deviation of ±1.0%) in this region of the GPR-SER plane, that is, ((1.319-1.22)/1.22)*100. It was a little larger for the most difficult vowel /o/ (9.5%) and a little smaller for the easiest vowels /a/ (7.1%) and /e/ (7.3%). For comparison, the JNDs for noise level (loudness), light level (brightness) and chemical density (odour) are about 10%, 15% and 25% respectively (Miller, 1947; Cornsweet and Pinsker, 1956; Gescheider, 1976). The JND for speaker size is approximately the same for the six conditions where the GPR is either 40 or 160 Hz (two left columns of the design cf. Fig. 1), being on average about 9%. When the pitch is 640 Hz, the JND doubles to about 18% when the SER is greater than 1. For the condition with a high pitch and a long VTL (Fig. 1 bottom-right point), the task essentially breaks down. The JND was measurable for three of the listeners but it rose to 50%, and two of the listeners could not do the task. The pattern of size discrimination performance is related to recognition performance (cf. section C). Briefly, discrimination performance is good where recognition performance is good and vice versa. Notably, discrimination does not deteriorate as soon as the GPR and VTL values exceed the normal speech range (shown by the ellipse in Fig. 1). For comparison, the JND for pitch discrimination was measured for these same vowels at five of the nine points where size discrimination was measured – the central point and the four corners (cf. Fig. 1). The JND for GPR discrimination was less than 2% when the GPR was greater than 100 Hz, independent of VTL. The JND rises to about 9% when the GPR is 40 Hz, both for long and short vocal tracts. In this region, the GPR is approaching the lower limit of melodic pitch, which is about 32 Hz (Pressnitzer et al., 2001), and the JND for discrimination of a change in the rate of clicks in a click train rises to values of about 7% (for a recent review, see Krumbholtz et al., 2000). The JND for the frequency of a sinusoid also rises as frequency decreases below 250 Hz (e.g. Sek and Moore, 1995). Thus GPR and size discrimination show different patterns of variation across the GPR-SER plane. GPR discrimination deteriorates in a region where size discrimination remains good (i.e., the region of low pitch), and GPR discrimination remains good in the region where size discrimination deteriorates (i.e., for combinations of high pitch and long vocal tract). In the single-vowel discrimination experiment, the listeners reported using speaker size as the cue for the discrimination rather than the pitch of a sinusoid. Nevertheless, it would be possible to do the task using a simple spectral cue if one could reliably identify the spectral peak associated with one of the formants in the first interval and check to see which way it shifted in the second. It is our opinion that this is not possible when the vowel and pitch change on every trial. The speech-like discrimination task effectively precludes the possibility of making the size discrimination on the basis of a simple spectral cue. The JND for speaker size was measured with the speech-like paradigm with four vowels in each interval and varying pitch contours in the two intervals (Fig. 2). The size JND was measured at the center point of the normal range and for two concentric squares of 8 points centered on the first point; the outer square is composed of the 8 points in the single-vowel experiment; the inner square has a positive diagonal that just encompasses the normal range of GPR-SER values in speech. The circles in Fig. 1 show the specific combinations. The JND for speaker size was measured at seventeen points in the GPR-SER plane, which is sufficient to make a contour map of resolution. Figure 5 shows the speaker-size JND (SER JND in percent) as a function of GPR and SER with logarithmic axes using a 2D surface plot in which grey tone shows resolution. Small JNDs (better resolution) are plotted in greys approaching white and large JNDs (worse performance) are plotted in greys approaching black. The actual sample points are shown as circles; the contours are derived by interpolation between the data points. The three ellipses show estimates of the normal range of GPR and SER in speech for men, women and children (Peterson and Barney, 1952). In each case, the ellipse encompasses 90% of the individuals in the Peterson and Barney data for that category of speaker (man, woman or child). Figure 5 and Table 1 show that discrimination performance is excellent, with JNDs less than 10%, in a triangular region of the GPR–SER space that includes about half of the normal region for women and children and most of the normal region for men. The 15% and 20% contours shows that discrimination performance remains high for SERs well beyond the normal range, provided the GPR is below about 200 Hz. Above 200 Hz, the 15% and 20% contours are well outside the normal range for short vocal tracts, but the 15% contour encroaches on the normal range for women and children when the vocal tract is relatively long. We were unable to measure the JND in the bottom, right-hand condition (640 Hz, 0.67 SER). In this case, the F0 of the GPR is above the first formant, causing the vowel quality to deteriorate. To anchor the contour map in the bottom-right corner, we used the JND from the single-vowel discrimination experiment. Typically, JND values obtained with the single-vowel paradigm were slightly better than in the speech-like paradigm, so performance in this corner may be even worse than that shown.
Vowel Recognition
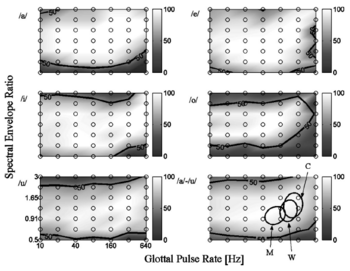
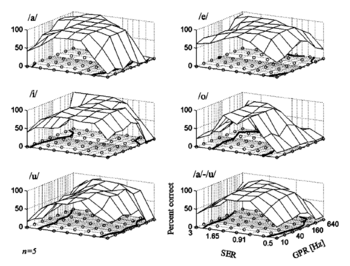
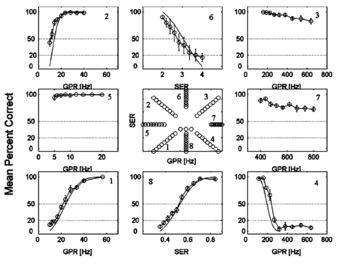
The vowel recognition data obtained with the surface paradigm are presented separately for the individual vowels in Fig. 6, along with the average for the five vowels (lower right-hand panel). The abscissa is GPR and the ordinate is SER plotted on logarithmic axes; the percent correct is given by the tone of grey. The points where performance was measured are shown by the circles. The grey-scale tone and contours were created by interpolation between the data points. The heavy black line shows threshold, that is, the 50 percent correct identification contour where d’ is 1.0 in this 5AFC paradigm. The figure shows that performance was surprisingly good and only drops below threshold for the more extreme values of GPR and SER. To reveal the regions where performance drops below ceiling levels more clearly, the data are also presented as 3-D surfaces in Fig. 7 plotted above a plane showing the sample points. The bold lines show the threshold contours as in Fig. 6. With regard to VTL, the worst performance is associated with the vowels /o/ and /u/, where both the upper and lower threshold contours fall just within the range of measured values. For /i/, the upper bound falls within the measured range; for /a/, the lower bound falls within the measured range. For /e/, performance only drops below threshold when low SER values occur in combination with either low or high GPR values. With regard to GPR, recognition performance remains near ceiling levels as GPR decreases below the range of voice pitch (~64 Hz), to the limit of melodic pitch (~32 Hz) and beyond. At 10 Hz, although there is no pitch sensation and one hears a stream of individual glottal cycles, the vowel quality is readily perceived. As GPR increases above the normal speech range to 640 Hz, performance remains near ceiling levels for /a/, /i/ and /u/. Performance drops to threshold irregularly along the upper GPR boundary for /e/ and it drops reliably below threshold for one vowel, /o/. The average data present a reasonable summary of recognition performance for the five vowels (lower right-hand panel). Performance drops to threshold when the SER value decreases to ~0.6 or when it increases to ~2.8, and this is largely independent of GPR. Between the threshold SER contours, performance is similar for GPR values throughout the range from 10 to 640 Hz. The recognition data obtained with the strip paradigm are presented separately for the eight strips in the panels around the circumference of Fig. 8; the center panel shows the GPR-SER values for each strip. The data are averaged over vowel type. The ordinate is mean percent correct in all of the data panels. The abscissa is GPR for the panels in the left-hand and right-hand columns of the figure; the abscissa is SER in the two data panels in the central column of the figure. Threshold for these psychometric functions is 50 percent correct where d’ is 1.0 in this 5AFC paradigm. The data panels in the central row of the figure show that for a central SER value, performance stays above threshold throughout the full range of GPR values from 5 to 640 Hz; indeed, at the lower GPR values, performance is essentially perfect even in the region below the lower limit of pitch. The data panels in the central column of the figure show that for a pitch of 80 Hz (very low male), performance stays above threshold down to an SER value of 0.55 and up to an SER value of 2.8. If the recognition surface were elliptical in shape, reflecting the shapes of the normal ranges for men women and children, then the psychometric functions across the top and bottom rows would have the same form and drop to threshold in approximately the same region of the figure. By and large, they do not. In the top row, performance remains well above threshold for the high GPRs in the right-hand panel, and it only just drops to threshold for the low GPRs in the left-hand panel. For short VTLs, then, the shape of the recognition surface is more rectangular than elliptical. In the bottom row, left-hand panel, the psychometric function falls below threshold in about the same region as the psychometric function in the central panel indicating that GPR and SER interact when both values are small to produce a larger reduction in performance than either would on its own; this means that the corner of the recognition surface is rounded in this case. In the bottom right-hand panel, the psychometric function falls below threshold even sooner than the psychometric function in the central panel indicating that GPR and SER interact more strongly here and produce a much larger reduction in performance than either would on its own; this means that this corner of the recognition surface is more rounded than the surface in Fig. 6 might initially indicate. This is because it is difficult to produce vowels with a well defined first formant when the GPR is high.
Speaker-size discrimination and vowel recognition performance
Table 1 shows that speaker size discrimination and vowel recognition performance are related; when discrimination performance is good, vowel recognition performance is good. As we move away from the normal speech range (cf. ellipses in Figs 5 and 6) performance starts to drop off in a similar way for both perceptual tasks. The Pearson product-moment coefficient of correlation, r, between these two performance measures is -0.91 and it is highly significant (p << 0.001, one-tailed, N=17). The negative correlation is because high vowel recognition scores go with low speaker-size JNDs.
Discussion
The discrimination experiments show that listeners can make fine judgements about the relative size of two speakers, and that they can make size judgements for vowels scaled well beyond the normal range in both VTL and GPR (Fig. 5). The JND for SER is less than 10% over a wide area of the GPR-SER plane, and when the GPR is 160 Hz, there are approximately 10 JNDs in speaker size between the bounding SER values of 0.67 and 2.23. The recognition experiments show that listeners can identify vowels manipulated to simulate speakers with GPRs and VTLs well beyond the normal speech range (Fig. 6). Recognition performance was above threshold for an area approximately ten times greater than the normal speech range.
Speaker-size discrimination
The most relevant data on size perception come from some simple studies performed by Lass and Davis (1976) and Fitch (1994). Lass and Davis (1976) asked listeners to judge the height of 30 men and women reading a standard prose passage on a four category scale. Categorization performance was better than chance. However, no attempt was made to control for the average pitch difference between men and woman, and the range of heights was limited. Fitch (1994) used computerized vowel sounds. He made the assumption that formant frequencies are a linear function of VTL and scaled the formant values for an 18 cm vocal tract to produce proportional values for vocal tracts of 17, 16 and 15 cm. For each vocal tract, he synthesized the “schwa” vowel at two GPRs, 100 and 150 Hz. The vowels were presented one at a time to a group of listeners who rated the size of the speaker on a 7-point scale. Despite the simplicity of the experiment and the limited range of VTL values, the data show significant main effects of both GPR and VTL on the size ratings for this schwa vowel. The dissertation does not, however, measure size discrimination or vowel recognition, and the vowels are limited to the normal range for men. The acoustic basis for size discrimination is clear; formant frequencies decrease as VTL increases. Research on speech production indicates that, over the full range of size from children to adults, the relationship between formant frequency and VTL is almost linear (Fant, 1960). Measurements with magnetic resonance imaging (Fitch and Giedd, 1999) show that VTL is highly correlated with height (Fitch and Giedd, 1999). There is also a highly significant correlation between formant frequency and age (Huber et al., 1999). Recently, González (2004) has reported that there is even a weak relationship between formant frequency and size within a group of adult men and within a group of adult women. Turner and Patterson (2003) have recently used quantitative clustering to reanalyse the classic data of Peterson and Barney’s (1952) and show that within a given vowel cluster, speaker size is the largest source of variation. Finally, it is perhaps worth noting that there is a strong relationship between formant related parameters and body size in rhesus monkeys (Fitch, 1997). In retrospect, given the importance of body size in human interaction, and the strong correlation between height and vocal tract length (Fitch and Giedd, 1999), it seems odd that the perception of speaker size has received so little attention in hearing and speech research. In spectral terms, the effect of a change in speaker size is theoretically very simple; if the GPR is fixed and the frequency axis is logarithmic, the profile for a given vowel has a fixed shape and VTL changes simply shift the profile as a unit – towards the origin as size increases and away from it as size decreases. The analysis of spectral profiles by the auditory system has been a very popular topic in psychoacoustics since it was introduced by Spiegel, Picardi and Green (1981). However, in the main, people have elected to follow Spiegel et al. and concentrate on profiles constructed from sets of equal-amplitude sinusoids whose frequencies are equally spaced on a logarithmic axis. These stimuli are not like the voiced parts of speech; they do not have a regular harmonic structure, the excitation is not pulsive, and they sound nothing like vowels. Moreover, the task in traditional Profile Analysis (PA) is to detect an increment in one of the sinusoidal components, which is very different from detection of a shift in the spectral location of the profile as a whole. An excellent overview of PA research is presented in Drennan (1998) and he describes a few PA experiments in which the stimuli are composed of sets of harmonically related components that are intended to simulate vowel sounds to a greater or lesser degree. Leek, Dorman and Summerfield (1987) generated four “flat-spectrum vowels” starting with a set of equal-amplitude harmonics spanning much of the speech range, and incremented pairs of components at the frequencies of the formant peaks. They measured the size of the increment required to recognize the vowel and found it to be consistent with the results of traditional profile studies as reported in Green (1988). Alcántara and Moore (1995) generated six flat-spectrum vowels with the components in cosine phase, as they are in normal vowels, or with the components in random phase. As might be expected, the increment required at the formant frequencies to detect the vowel was consistently smaller in the cosine-phase condition than in the random-phase condition. However, in these and other PA studies, there is no attempt to simulate the filtering action of the vocal tract and produce realistic vowel profiles; nor is there any attempt to simulate changes in VTL or measure sensitivity to coherent spectral shifts.
Vowel recognition
Assmann et al. (2002) have reported a recognition study similar to those presented in this paper in which the vowels of three men were scaled in GPR and SER using STRAIGHT. The SER was scaled up in five equal steps from 1.0 to 2.0. The GPR was scaled up in octaves from 1 to 2 and 4. The combinations of GPR and SER are presented by open squares in the upper panel of Fig. 3; in positioning the squares, it has been assumed that the average GPR and VTL for the 11 vowels of the three men is near the average GPR and VTL for men in the classic data of Peterson and Barney (1952). So the bottom square in the left column of squares is near the centre of the ellipse3 for men from the Peterson and Barney (1952) data. The recognition performance for the rectangle of the GPR-SER plane used in Assmann et al.’s experiment has the same general form as shown for our average data in the lower right-hand panel of Fig. 6 (labelled ‘/a/-/u/’). That is, when the GPR scalar is 1 or 2 and the SER is between 1.0 and 1.5, performance is at ceiling levels; thereafter, as the SER increases to 2.0, performance falls gradually, but it remains well above threshold for both GPR scalars (1 and 2). When the GPR scalar is 4, performance is at ceiling levels for the larger SER scalars (1.5 – 2.0) and it decreases as the SER scalar decreases to 1.0. That is, performance decreases as the stimuli encroach on the region where the definition of the first formant deteriorates (cf. dotted diagonal lines Fig. 3 upper panel). The percent correct values are lower in Assmann et al. (2002) than in our study because they used 11 vowel types rather than 5. Nevertheless, in the worst case (GPR scalar = 4; SER = 1), the d’ was 1.24 which is still above the threshold value (1.0) in Fig. 6 (bold solid line). Assmann et al. (2002) interpret the reduction in performance outside the range of GPR-SER combinations normally encountered for men women and children as evidence that the brain learns the combinations of pitch and formant frequencies associated with the different vowels for the normal range of men, women and children, in much the same way as a neural net would. The combinations of GPR and formant frequency in their experiment go beyond the normal range but not very far, and so in their next study (Assmann and Nearey, 2003), they extended the range taking the lowest GPR scalar down from 1.0 to 0.5 and the lowest SER down from 1.0 to 0.6. They used the vowels of two men, and extended the design with the vowels from two women and two children (aged 7). Reducing the GPR scalar to 0.5 has essentially no effect on performance relative to that achieved with a GPR scalar of 1.0; this is true for all values of SER and for all three classes of speaker. Similarly, the effect of reducing the SER is small when the GPR scalar is 0.5 or 1.0; there is a reduction in performance for the vowels of the men and women, but it remains well above threshold. The most striking effect is a three-way interaction between GPR scalar, SER and speaker group. Briefly, when the GPR scalar is 0.5 or 1.0, the reduction in performance observed with the vowels of men as SER rises to 2.0, is accentuated with the vowels of women and children, and when the GPR scalar is increased to 4, the effects of SER and speaker class are amplified and performance drops to chance. Much of the complexity, however, appears to be the result of using relative measures for GPR and VTL when plotting the data, and ignoring the fact that the base values of GPR and SER are changing substantially across speaker group in the statistical analysis. The asterisks in Fig. 3 show the combinations of GPR and SER for the data of Assmann and Nearey (2003) when we adjust for the fact that the base GPR (1.0) represents a higher pitch for women and children, and the base SER (1.0) represents a shorter vocal tract for women and children. Specifically, we assume that the origin for each speaker group (GPR scalar = 1; SER = 1) is at the center of the Peterson and Barney ellipse for that group. This shows that when the GPR scalar is 4, the vowels for women and children (right-most pair of asterisk columns) are in the region where the definition of the first formant is deteriorating (cf. diagonal lines Fig. 3), and the vowels for men (column of asterisks at GPR ~ 600 Hz) are encroaching on this region. For the remainder of their conditions, performance is well above threshold, except for the largest SER (2.0) for women and children, and in this region performance is deteriorating in our data as well. In summary, the pattern of recognition performance in the region where the data overlap appears to be comparable in all three of these recognition experiments.
Vowel normalization by scale transform and/or statistical learning
There are several aspects of the recognition data which suggest that performance is not primarily determined by learning the statistics of the correspondence between GPR and formant frequencies in natural speech with a neural net as suggested by Assmann et al. (2002). Neural nets have no natural mechanism for extrapolating beyond the training data (LeCun and Bengio, 1995; Wolpert, 1996a,b), so we would expect some deterioration in recognition performance as soon as either the GPR or SER move beyond the normal range. Assmann and colleagues do not provide a clear specification of the normal range, but it would seem reasonable to assume that theirs would be similar to the one we derived from the Peterson and Barney (1952) data. A comparison of the data from all three recognition experiments with the ellipses of normal GPR and SER values (cf. Figs 3 and 6) shows that recognition performance is near to ceiling levels across a region of GPRs and SERs that extends well beyond the normal range. This includes many physiologically implausible combinations that most people would have little or no experience of. Most notably, performance does not drop as GPR decreases down out of the normal range for men, women or children. It remains at ceiling levels down to the lower limit of voice pitch. Much of the drop in recognition performance in the studies of Assmann and colleagues occurs, as in our study, in the region where it is not possible to generate vowels with a good definition of the first formant (bottom right-hand corners of the panels in Fig. 6). The formant is only represented by one harmonic (the fundamental) on the upper side of the formant. It seems likely that this plays at least as large a role in the reduction of performance as lack of experience of vowels in this region. While we do not wish to deny a role for experience and training in improving performance in vowel recognition, it is hard to see it explaining the large range over which listeners are able to recognize vowels at near ceiling levels, particularly when they are given no feedback. Assmann and colleagues do not consider the possibility that the auditory system applies a scale transform to the internal representation of sound prior to the recognition process as suggested by Cohen (1993) and Irino and Patterson (1999b, 2002), and that the normalization inherent in the scaling transform is the reason why humans can recognize vowels with GPRs and VTLs far beyond the normal speech range. Our data showing that size discrimination and vowel recognition are both possible over a region approximately ten times greater than the normal speech range supports the hypothesis that the auditory system applies some form of scaling transform (such as the Mellin transform) to all input sounds prior to speech-specific processing. There are two complimentary advantages provided by scale transforms which segregate the size information associated with vocal tract length from the shape information associated with vowel type: on the one hand, the normalization renders vowel recognition immune to size distortion and facilitates the problem of dealing with speakers of very different sizes; on the other hand, it concentrates the size information in the representation and facilitates decisions such as whether the speaker is a man, woman or child. Recently, the Auditory Image Model (AIM) of Patterson et al. (1992, 1995) has been extended to include a stage that normalizes the auditory images produced by AIM and converts them to Mellin Images which are scale invariant. The system was tested with the aid of a simple vowel classifier and a large range of scaled vowels like those in the current experiments (Turner et al., 2004). The tests showed that the recognition of scaled vowels is enhanced by the addition of the Mellin Image stage, and the range of supra-threshold performance is compatible with our vowel recognition data. This adds further support to the hypothesis that the auditory system has a scaling mechanism and that it plays an important role in vowel normalization.
Relative versus absolute size
It is important to distinguish between judging relative size and absolute size. Our discrimination task only requires a relative size judgement; moreover, the two sounds are presented in a paradigm designed to favour the immediate comparison of two internal representations of sound and minimize the memory load. It is like judging which of two weights is heavier by lifting one and then the other; you do not need to know what the absolute weights are, simply that the second feels lighter or heavier when you pick it up. Judgements about absolute size are probably much harder to make, and it seems likely that you need to know something about the source to judge its absolute size. The general problem of the relationship between the perception of relative and absolute size is beyond the scope of this paper.
Summary and Conclusions
The Mellin transform has been used to develop a signal-processing model of vowel normalization (Cohen, 1993) and an auditory model of vowel normalization (Irino and Patterson, 2002). The implication is that size is a dimension of sound and that the size information can be segregated automatically from the shape information. The current paper presents psychophysical experiments which suggest that size is a dimension of auditory perception as well as a dimension of sound itself, and that vowel normalization is based on a scale transform. Glottal pulse rate and vocal tract length were manipulated independently over a large range using a high-quality vocoder (STRAIGHT). Human listeners were able to make discriminations about speaker size, and to recognize scaled vowels, over a range of GPRs and SERs ten times greater than that encountered in normal speech (Figs 5 and 6). The results support the hypothesis that the auditory system includes some form of scale transform that automatically segregates size and shape information in the sound.
Acknowledgements
This research was supported in part by the following institutions: (authors DS, RP, RT) the UK Medical Research Council (G9901257) and the US EOARD (Contract No. SPC-024083); (author HK) the National Institute of Information and Communications Technology of Japan; (author TI) faculty of systems engineering, Wakayama University, and the Japanese Ministry of Education, Science, Sports and Culture, Grant-in-Aid for Scientific Research (B), 15300061, 2003. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of EOARD. Pilot data from this research programme was reported in Turner et al. (2004). Some of the work has been reported in abstract form (Smith, Patterson and Jefferis, 2003; Smith and Patterson, 2004).
Notes
1http://www.mrc-cbu.cam.ac.uk/cnbh/web2002/framesets/Soundsframeset.htm. Click on “Scaled vowels”.
2 An estimate of the size of speaker for a given SER can be derived by extrapolating from the VTL versus height data in Fitch and Giedd (1999). The average VTL for 7 men aged 19 to 25 in Fitch and Giedd (1999) was 16 cm. An SER of 0.5 means that the spectrum envelope of the initial input vowel has been compressed by a factor of two while an SER of 3.0 means that the spectrum envelope has been dilated by a factor of three. Assuming linear scaling between formant position and VTL, our SERs are equivalent to VTLs of 32 cm (giants) and 5.3 cm (tiny children). Given the correlation between VTL and height (Fitch and Giedd, 1999 cf. Fig. 2a), our smallest SER of 0.5 would simulate the sound of a speaker 4.3 m (14 feet) tall, and our largest SER of 3.0 would simulate a baby just 0.35 m (1 foot 2 inches) tall.
3 The open square symbols for Assmann et al. (2002) have been slightly displaced to the left by 15, 30 and 40 Hz for the first, second, and third columns, respectively, to distinguish them clearly from some of the asterisks symbols used for Assmann and Nearey (2003).
References
Alcántara, J. I., and Moore, B. C. J. (1995). “The identification of vowel-like harmonic complexes: effect of component phase, level and fundamental frequency,” J. Acoust. Soc. Am. 97, 3813-3824.
Assmann, P. F., Nearey, T. M., and Scott, J. M. (2002). “Modeling the perception of frequency-shifted vowels,” in Proceedings of the 7th Int. Conference on Spoken Language Perception, ICSLP, 425-428.
Assmann, P. F., and Nearey, T. M. (2003). “Frequency shifts and vowel identification,” in Proceedings of the 15th Int. Congress of Phonetic Sciences, Barcelona ICPhS.
Clutton-Brock, T. H., and Albon, S. D. (1979). “The roaring of red deer and the evolution of honest advertising,” Behaviour 69, 145-170.
Cohen, L. (1993). “The scale transform,” IEEE Trans. Acoust. Speech and Signal Process. 41, 3275-3292.
Cornsweet, T. N., and Pinsker, H. M. (1965). “Luminance discrimination of brief flashes under various conditions of adaptation,” J. Physiol. (London) 176, 294-310.
Drennan, W. (1998). “Sources of variation in profile analysis: individual differences, extended training, roving level, component spacing and dynamic contour,” Unpublished Ph.D. Dissertation, Indiana University.
Dudley, H. (1939). “Remaking speech,” J. Acoust. Soc. Am. 11, 169-177.
Fant, G. (1960). Acoustic theory of speech production. (The Hague: Mouton & Co.).
Fairchild, L. (1981). “Mate selection and behavioural thermoregulation in Fowler’s toads,” Science 212, 950-951.
Fitch, W. T. (1994). “Vocal tract length perception and the evolution of language,” Unpublished Ph.D. Dissertation, Brown University.
Fitch, W. T. (1997). “Vocal tract length and formant frequency dispersion correlate with body size in rhesus macaques,” J. Acoust. Soc. Am. 102, 1213-1222.
Fitch, W. T., and Giedd, J. (1999). “Morphology and development of the human vocal tract: A study using magnetic resonance imaging,” J. Acoust. Soc. Am. 106, 1511-1522.
Foster, D. H., and Bischof W. F. (1997). “Bootstrap estimates of the statistical accuracy of thresholds obtained from psychometric functions,” Spatial Vision 11, 135-139.
Gescheider, G. A. (1976). Psychophysics; Method and theory. (Lawrence Erlbaum Associates, Hillsdale N. J).
González, J. (2004). “Formant frequencies and body size of speaker: a weak relationship in adult humans,” J. Phonetics 32, 277-287.
Green, D. M. (1988). Profile Analysis (Oxford University Press, London).
Huber, J. E., Stathopoulos, E. T., Curione, G. M., Ash, T. A., and Johnson, K. (1999). “Formants of children, women and men: The effects of vocal intensity variation,” J. Acoust. Soc. Am. 106, 1532-1542.
Irino, T., and Patterson, R.D. (1997). "A time-domain. level-dependent auditory filter: the gammachirp," J. Acoust. Soc. Am. 101, 412-419.
Irino, T., and Patterson, R. D. (1999a). “Extracting size and shape information of sound sources in an optimal auditory processing model,” CASA Workshop, IJCAI-99, Stockholm, Aug., 1-4.
Irino, T., and Patterson, R. D. (1999b). “Stabilised wavelet Mellin transform: An auditory strategy for normalising sound-source size,” Eurospeech 99, Budapest, Hungary, Sept., 1899-1902.
Irino, T., and Patterson, R. D. (1999c). “An auditory strategy for separating size and shape information of sound sources,” Japan Soc. Artificial Intell., Tech. Rep., SIG-Challenge-9907-6, 33-38.
Irino, T., and Patterson, R. D. (2002). “Segregating information about the size and shape of the vocal tract using a time-domain auditory model: The stabilised wavelet-Mellin transform,” Speech Communication 36, 181-203.
Kawahara, H., Masuda-Kasuse, I. and de Cheveigne, A. (1999). "Restructuring speech representations using pitch-adaptive time-frequency smoothing and instantaneous-frequency-based F0 extraction: Possible role of repetitive structure in sounds," Speech Communication