The Size Information in Communication Sounds
From CNBH Acoustic Scale Wiki
Roy Patterson , David R. R. Smith, Ralph van Dinther, Tom Walters
Contents |
Introduction
This Chapter is about the perception of the sounds that animals use to communicate at a distance, and the information that these sounds convey about the animal as a source. Broadly speaking, these are the sounds that animals use to declare their territories and attract mates, and the focus of the chapter is the size information in these sounds and how it is perceived. The sounds produced by the sustained-tone instruments of the orchestra (brass, strings and woodwinds) have a similar form to the communication sounds of animals, and they also contain information about the size of the source, that is, the specific instrument type (e.g. violin or cello) within an instrument family (e.g. strings). Animals and instruments produce their sounds in very different ways, and the comparison of these two major classes of communication sounds reveals the general principles underlying the perception of source size in communication sounds.
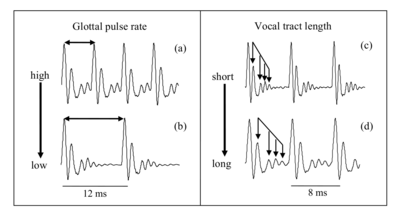
For humans, the most familiar communication sound is speech, and it illustrates the fact that communications sounds contain information about the size of the source. When a child and an adult say the ‘same’ word, it is only the linguistic message that is the same. The child has a shorter vocal tract and lighter vocal cords, and as a result, the waveform carrying the message is quite different for the child. The situation is illustrated in Figure 1 which shows short segments of four versions of the vowel in the word ‘mama’. From the auditory perspective, a vowel is a ‘pulse-resonance’ sound, that is, a stream of glottal pulses each with a resonance showing how the vocal tract responded to that pulse. From the perspective of communication, the vowel contains three important components of the information in the sound. The first component is the ‘message,’ which is that the vocal tract is currently in the shape that the brain associates with the phoneme /a/. This message is contained in the shape of the resonance which is the same in every cycle of all four waves. The second component of the information is the glottal pulse rate. In the left column, an adult has spoken the /a/ with a fast glottal pulse rate (a) and then a slow glottal pulse rate (b). The glottal pulse rate determines the pitch of the voice. The resonances are identical since it is the same person speaking the same vowel. The third form of information is the resonance rate. In the right column, the same vowel is spoken by a child with a short vocal tract (c) and an adult with a long vocal tract (d) using the same glottal pulse rate. The glottal pulse rate and the shape of the resonance (the message) are the same, but the rate at which the resonance proceeds within the glottal cycle is faster in the upper panel. That is, the resonances of the child ring faster, both in terms of the resonance frequency and the decay rate. In summary, the stationary segments of the voiced parts of speech carry three forms of information about the sender – information about the shape of the vocal tract, its length, and the rate at which it is being excited by glottal pulses.
The components of the vocal tract (the nasal, oral and pharyngeal passages) are tubes that connect the openings of the nose and mouth to the trachea and the oesophagus. They are an integral part of the body and they increase in length as the body grows. The decrease in pulse rate and resonance rate that occurs as humans grow up is a general property of mammalian communication sounds. Section 2 of this chapter describes the form of pulse resonance sounds and Section 3 describes how information about source size is coded in these sounds. The fact that we hear the same message when children and adults say the same word suggests that the auditory system has mechanisms to adapt the analysis of speech sounds to the pulse rate and resonance rate, as part of the process that produces the size invariant representation of the message. This suggests that there are an initial set of auditory processes that operate like a preprocessor to stabilize repeating neural patterns and segregate the pulse-rate and resonance-rate information from the information about the message. Irino and Patterson (2002) have demonstrated how these processes might work. First, the auditory system adapts the analysis to the pulse rate using ‘strobed temporal integration.’ Then the resulting ‘auditory image’ is converted into a largely scale-invariant Mellin Image with the aid of resonance-rate normalization. As a by-product, the two processes produce a contour of pulse-rate information and a contour of resonance-rate information that the listener can use to estimate speaker size, and to track individual speakers in a multi-source environment. Section 4 of the Chapter illustrates the representation of size information in the auditory system.
Communication Sounds
Pulse-resonance sounds are ubiquitous in the natural world and in the human environment. They are the basis of the calls produced by most birds, frogs, fish and insects, as well as mammals, for messages that have to be conveyed over a distance, such as those involved in mate attraction and territorial defence (e.g. Fitch and Reby 2001). They are also conceptually very simple. The animal develops some means of producing a pulse of mechanical energy which causes structures in the body to resonate. From the signal processing perspective, the pulse marks the start of the communication and the resonances provide distinctive information about the shape and structure of parts of the sender’s body, and thus, the species producing the sound. The pulse does not contain much information other than the fact that the communication has begun. Its purpose is to excite structures in the body of the animal which then resonate in a unique way. The resonance has less energy than the pulse but more information; it follows directly after the pulse and acts as though it is attached to it. So the location of the species-specific information is very predictable; it is tucked in behind each pulse.
In human speech, the vocal folds in the larynx at the base of the throat produce a pulse by momentarily impeding the flow of air from the lungs; this pulse of air then excites complex resonances in the vocal tract above the larynx. The mechanism is described in the next Section. The mechanism is essentially the same in all mammals, and there is a similar mechanism in many birds and frogs; they both excite their air passages by momentarily interrupting the flow of air from the lungs. Fish with swim bladders often have muscles in the wall of the swim bladder (e.g. the weakfish, Cynoscion Regali) that produce brief mechanical pulses, referred to as ‘sonic twitches’ (Sprague 2000), and these twitches resonate in the walls of the swim bladder which makes the combination distinctive. Note that the sound producing mechanisms in these four groups of vertebrates (fish, frogs, birds and mammals) probably all evolved separately; the swim bladder mechanism in the fish did not evolve into the vocal tract mechanism of the land animals, and the vocal tract mechanisms do not appear to have developed one from another. The implication is that this is convergent evolution, with nature repeatedly developing variations of the same basic solution to acoustic communication – the combination of a sharp pulse and a body resonance.
The sustained-tone instruments of the orchestra (brass, strings and woodwinds) are also excited by non-linear processes that produce sharp pulses which resonate in the air columns, or air cavities, of the instruments (Fletcher and Rossing 1998); so they also produce pulse resonance sounds (van Dinther and Patterson 2006). Combustion engines produce mini-explosions that resonate in the engine block; so they are also pulse-resonance sounds. They are not communication sounds in the normal sense, but they show that the world around us is full of pulse-resonance sounds, which the auditory system analyses automatically and effortlessly.
There are also many examples of communication sounds that consist of a single pulse with a single resonance: Gorillas beat their chests with cupped hands, elephants stomp on the ground, and blue whales boom. Chickens and lemurs cluck every few seconds as they search for food in leaf litter. Humans clap their hands to attract attention. The percussive instruments like xylophones, wood blocks and drums also produce single-cycle, pulse-resonance sounds. These percussive sources produce very different sounds from those of animals and sustained-tone instruments because the resonance occurs within the material of the bar, or plate, rather than in an air column, or air cavity, in an animal or instrument. The materials of the bars and plates (typically metal or wood) are dense and stiff, and so the resonances ring much longer in these sources. Nevertheless, they are pulse-resonance sources and the principles of sound production and perceptual normalization are similar to those for the sustained-tones produced by speech and music sources.
The variety of these pulse-resonance sounds, and the fact that humans distinguish them, is illustrated by the many words in our language that specify transient sounds; words like click, crack, bang, thump, and word pairs like ding/dong, clip/clop, tick/tock. In many cases, a plosive consonant and a vowel are used to try and imitate some property of the pulse-resonance sound.
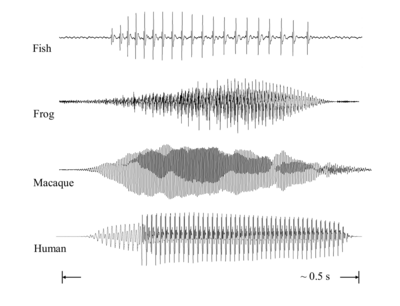
Finally, it should be noted that in the world today, most animals produce their communication sounds in the form of what might be called pulse-resonance ‘syllables’, that is, streams of regularly timed pulses, each of which carries a copy of the resonance to the listener. The syllables are on the order of 200-800 ms in duration, with a pulse rate in the region 10 to 500 Hz. The pulse rate rises a little at the onset of the sound, remains fairly steady during the central portion of the sound, and drops off with amplitude during the offset of the sound, which is typically longer and more gradual than the onset. A selection of four of these animal syllables is presented in Figure 2; they are the calls of (a) a Mongolar drummer, or Jamaica weakfish (Cynoscion, jamaicensis), (b) a North American Bull frog (Lithobates, catesbeiana), (c) a macaque (Macaca, mulatta), and (d) a human adult saying /ma/1.
The sounds may be played and/or downloaded.Mongolar drummer fish
|
Bull frog
|
Macaque
|
Human
|
The notes of sustained-tone instruments are like animal syllables with fixed pulse rates and comparatively flat temporal envelopes. Both of these classes of communication sound are completely different from the sounds of inanimate sources like wind and rain which are forms of noise. In the natural world, the detection of a pulse-resonance sound in syllable form immediately signals the presence of an animate source in the local environment.
Size Information in Communication Sounds
The Effect of Source Size in Vocal Sounds
In general, as a mammal matures and becomes larger, there is a consistent and predictable decrease in both the resonance rate and the pulse rate of their communication sounds, primarily because they are produced by structures that increase in size as the animal grows. The vibration of the vocal tract of a mammal is often modelled in terms of the standing waves that arise in a tube closed at one end (Chiba and Kajiyama 1942; Fant 1960). The resonances of the vocal tract are referred to as formants and the resonance rate of the lowest formant, F1, is determined by the longest standing wave in the vocal tract. The relationship between resonance rate and standing-wave length for the first formant is
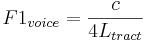
where c is the speed of sound in air (340 m/s) and Ltract is the length of the vocal tract which can be as long as 17 cm in tall men. So the frequency of the first formant for men is on the order of 500 Hz (340/4. 0.17). The point to note is that the size variable, Ltract, is in the denominator on the right-hand side of the equation, which means that, as a child grows up into an adult and the length of their vocal tract increases, the resonance rate of the first formant decreases. This is a general principle of formants and of mammalian communication sounds.
The vocal cords produce glottal pulses in bursts and the vibration of the vocal cords can be modelled by the equation for the vibration of a tense string, although the vocal cords are actually rather complicated structures. The glottal pulse rate, F0voice, is the fundamental mode of vibration of the vocal cords, and the relationship between glottal pulse rate and the properties of a tense string are
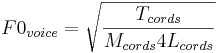
where Tcords, Mcords and Lcords are the Tension, Mass and Length of the vocal cords. In this case, there are two physical variables associated with size; they are the length of the vocal cords and their mass; both increase as a child grows up. The point to note is that both mass and length terms are in the denominator on the right-hand side of the equation, and they combine multiplicatively, so increases in size, be it length or mass, lead to a decrease in glottal pulse rate. The average F0voice for children is about 260 Hz, and it decreases progressively to about 120 Hz in adult men. The reduction in pulse rate with increasing size is also a general principle of mammalian communication sounds. Thus, when we encounter a new species of mammal, we do not need to learn about the relationship between their calls and their size. If the syllables of one individual have a consistently lower pulse rate and a consistently lower resonance rate than the syllables of a second individual, then we can predict with reasonable confidence, that the first individual is larger, without ever having seen a member of the species
Speakers can also vary the tension of the vocal cords and change the pitch of the voice voluntarily. They do this to make prosodic distinctions in speech; for example, in many European languages, speakers raise the pitch of the voice at the end of an utterance to indicate that it is a question. This is also how singers change their pitch to produce a melody. The voluntary variation of tension makes the use of pulse rate as a size cue somewhat complicated. But basically, for a given speaker, the long-term average value of their voice pitch over a sequence of utterances, is size information rather than speech information. Whereas, the short-term changes in pitch over the course of an utterance are speech information (prosody) rather than size information.
Finally, note that, in pulse-resonance sounds, the frequency of the resonance is always greater that the pulse rate; this is one of the defining characteristics of the sounds used by mammals for communication.
The Effect of Source Size in Musical Instrument Sounds
The instruments of the orchestra are grouped into ‘families’ (e.g. brass, strings, etc.). The members of a family (e.g. trumpet, French horn and tuba) have similar construction and they produce similar sounds; they differ primarily in their size. The mechanisms whereby sustained-tone instruments (the brass, string and woodwind families) produce their notes are quite different from each other, and quite different from the way mammals produce syllables. Nevertheless, the excitation in sustained-tone instruments is a regular stream of pulses (Fletcher and Rossing 1998), each of which excites the body resonances of the instrument, As a result, sustained-tone instruments produce pulse-resonance sounds (van Dinther and Patterson 2006), and the sounds reflect the size of the source both in their pulse rate and their resonance rate, albeit in rather different ways than for the voice.
The French horn illustrates the form of the size information. It is a tube closed at one end like the vocal tract, and so the equation that relates fundamental frequency to tube length is the same as the one used to specify the frequency of the first formant of the voice;
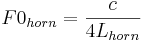
where Lhorn is the length of the brass tube when it is unrolled. However, in brass instruments, the length of the tube is associated with the pulse rate of the note rather than the frequency of the lowest body resonance. So the F0 is associated with the pitch of the note that the instrument is playing rather than its brassy timbre.
The relationship between the F0 of the instrument and the pulse rate at any particular moment is complicated by the fact the pulse rate is also affected by the tension of the lips, and the fact that it is not actually possible to excite the instrument with a pulse rate as low as its F0. The length of the French horn is about 3.65 m, so the F0 is about 23.3 Hz. This is actually below the lower limit of melodic pitch (Krumbholz et al. 2000; Pressnitzer et al. 2001). If for convenience, we think of this F0 as A0, then the instrument can be made to produce pulse rates which are harmonics of C1, beginning with C2, that is, C2, G2, C3, E3, G3, etc, by increasing the tension of the lips. The point of the example, however, is that the equation for pulse rate in brass instruments contains a size variable, e.g. Lhorn, and as the size of the instrument increases, the set of pulse rates that it produces decreases because the length of the tube is in the denominator on the right-hand side of the equation.
The broad mid-frequency resonance that defines the timbre of all brass instruments is strongly affected by the form of the mouth piece. When coupled to the tube of a brass instrument, the mouth piece can be modelled as a Helmholtz resonator (Fletcher and Rossing 1998). The vibration of a Helmholtz resonator is much more complicated than that of a tube, but it is nevertheless instructive with respect to the effects of source size on the acoustic variables of the French horn sound. If we designate the resonance frequency F1horn by analogy with F1voice, then the resonance rate of the formant is
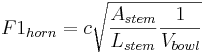
Astem and Lstem are the area and length of the stem which connects the bowl of the mouth piece to the tube, and Vbowl is the volume of the bowl of the mouth piece. This is a much more complex equation involving three size variables, and the balance of these variables is crucial to the sound of a brass instrument. For present purposes, however, it is sufficient to note that the most important size variable is the volume of the bowl and it is in the denominator; so once again, the rate of the body resonance decreases as the size of the bowl increases.
Similar relationships are observed in the other families of sustained-tone orchestral instruments, such as the woodwinds and strings; as the size of the components in the vibrating source and the resonant parts of the body increase, the pulse rate and the resonance rate decrease. This is the form of the size information in the sounds that animals use to communicate at a distance, and it is the form of the size information in the notes of sustained-tone instruments. Musical notes have a more uniform amplitude envelope and a more uniform pulse rate than animal syllables, and the range of size in these instrument families is typically greater than in mammalian species. Nevertheless, the size information has a similar form because of the basic properties of vibrating sources; as the components get larger in terms of mass, length or volume, they oscillate more slowly.
The same physical principles also to apply to the percussive sources described in Chapter 2, which produce single-cycle, pulse-resonance sounds. For example, in the equation that specifies the natural frequencies of a struck bar (Chapter 2, Eq. 3a), the length term is in the denominator, so the natural frequencies decrease as bar length increases. Similarly, in the equation for the natural frequencies of a struck plate (Chapter 2, Eq. 5), the length and width terms are both in the denominator. Thus, size information is ubiquitous in mechanical sound sources. We turn now to the perception of source size in speech sounds and musical sounds.
The Form of Size Information in the Human Auditory System
The representation of size information in the auditory system has been illustrated by Irino and Patterson (2002) using a pair of /a/ vowels like those in the right-hand column of Figure 1. The two vowels were simulated using the cross-area function of a Japanese male saying the vowel /a/ (Yang and Kasuya 1995). In one case, the vocal tract length was that appropriate for an average male (15 cm); in the other, the length was reduced by one third (10 cm) which would be appropriate for a small woman. The glottal pulse rate (GPR) was the same in the two vowels as it is in Figures 1c and 1d. The auditory image model (AIM, Patterson et al. 1992, 1995) was used to simulate the internal representation of the two vowels; the resulting ‘stabilized auditory images’ are shown in Figure 3 which is a modified version of Figure 3 in Irino and Patterson (2003). Briefly, a gammatone auditory filterbank is used to simulate the basilar membrane motion produced by the vowel, and the resulting neural activity is simulated by applying half-wave rectification and adaptive compression separately to each channel of the filterbank output (Patterson and Holdsworth 1996). The repeating waveform of the vowel sound produces a repeating pattern of neural activity in the auditory nerve. In AIM, the pattern is stabilized by (1) calculating time intervals from the neural pulses produced by glottal pulses, to the neural pulses produced by the remaining amplitude peaks within the glottal cycle, and (2) cumulating the time intervals in a dynamic interval histogram (one histogram for each channel of the filterbank). The result of this ‘strobed temporal integration’ (Patterson et al. 1992; Patterson 1994) is an array of dynamic interval histograms which is the auditory image; it is intended to simulate the first internal representation of the sound which you are aware of. The stabilization mechanism is assumed to be in the brainstem or thalamus.
The GPR of the synthetic /a/ vowels was 100 Hz, so the time between glottal pulses was 10 ms in both cases. The glottal pulses excite most of the channels in the filterbank, and so there are peaks at 0 ms and multiples of 10 ms in each channel, and these peaks form vertical ridges in the auditory image (Fig. 3). This is the form of voice pitch in the auditory image – a vertical ridge that moves left as pitch increases and right as pitch decreases. The single-cycle, pulse-resonance sounds described in Chapter 2 do not produce a vertical ridge in the auditory image and they do not produce the associated temporal pitch associated with the voice and sustained-tone instruments.
The rightwards-pointing triangles on the vertical ridges are the formants of the vowels in this representation (marked by F1-F4 and arrows). They show that the vocal tract resonates longer at these frequencies. The overall shape of the patterns is quite similar, since it is the same vowel, /a/. The formants in the right-hand auditory image are shifted up, as a unit, along the quasi-log-frequency dimension, and a comparison of the fine structure of the formants in the corresponding ellipses shows that the formants ring faster in the auditory image of the vowel from the shorter vocal tract. This is the form of a change in vocal tract length in the auditory image – the resonances move up as a group (that is, the resonance rates increase) and the resonances decay away faster so that the pattern shrinks in width. The same form of change occurs when the body resonators of musical instruments are reduced in size, and when the struck bars and plates described in Chapter 2 are reduced in size. In the latter case, the resonance structure is attached to the 0 ms vertical, and the resonance structure extends across the full width of the image because the density and stiffness of bars and plates mean that the resonances ring much longer than those in of the vocal tract or sustained-tone instruments.
The dimensions of the auditory image are both forms of frequency; the ordinate is acoustic frequency which for narrow resonators is the resonance rate; the abscissa is the reciprocal of pulse rate. So the auditory image segregates the two components of size information and presents them, as frequencies, in a simple orthogonal form. The time interval between the vertical ridges in the auditory image is directly related to the size of the vocal cords, through the speed of sound. The period of the individual resonances is directly related to the size of the resonators in the body of the source, again through the speed of sound. Thus, in this image, changes in the size of the excitation source are reflected in proportional changes in the time intervals between the vertical ridges, and changes in the size of the vocal resonators are reflected in proportional changes in the time-intervals in the triangular structures that represent the formants. Irino and Patterson (2002) and Turner et al. (2006) have demonstrated how the auditory image can be converted into a Mellin Image in which the pattern of the ‘message’, /a/, is truly scale invariant.
Finally note that, whereas strobed temporal integration preserves the details of the resonances as they arise in basilar membrane motion, pitch mechanisms based on autocorrelation and the autocorrelogram do not (Licklider 1951; Slaney and Lyon 1990; Meddis and Hewitt 1991; Yost et al. 1996). Autocorrelation averages periodicity information over the glottal cycle. Whenever the resonance period is not a sub-multiple of the glottal period, the periodicity information provided by the autocorrelation differs from the resonance rate of the formant. Thus, although autocorrelation can be used to predict the pitch and pitch strength of a vowel with great accuracy, the calculation smears the fine structure of the formant information (e.g. compare Figs 2c and 3c of Patterson et al. 1995), and consequently, it reduces the fidelity of any subsequent size-invariant representation of the message.
The pulse rate and resonance rate of a sound do not describe the size of a source in absolute terms. They are acoustic variables that describe properties of the sound wave as it travels from the sender to the listener. The acoustic variables change in a predictable way as the resonators in the sender’s body grow. However, the brain does not have the equations required to convert a pulse rate into a mass or a length, and even if it had the equation, there would still be difficulties. The information about all of the physical variables involved in the production of the sound has to be transmitted to the listener via only two acoustic variables, pulse rate and resonance rate. The acoustic variables often vary with the product of several physical variables like mass and length, so a given pulse rate could be produced by many different combinations of mass and length. So what the listener receives is one pulse rate value that summarizes the aggregate effect of all of the physical variables on the vibration source, and one resonance rate value that summarizes the aggregate effect of another set of physical variables on resonance rate.
Moreover, the brain is not actually interested in the mass, length or volume of the physical components of the sounder, such as the size of the vocal cords or the length of the vocal tract. What matters to the listener is the size of the sender’s body – some perceptual, and/or cognitive, combination of their height, mass and volume, and within a species, whether one sender is much bigger or smaller than another. In order to estimate the sender’s body size, a more central mechanism must combine the pulse-rate and resonance-rate information with some form of stored knowledge about the structure of the sender, and/or a body of experience with a range of individuals from the specific population.
Acknowledgements
Support for the writing of this paper and much of the research described in it was provided by the UK Medical Research Council (G990369, G0500221) and the German Volkswagen Foundation (VWF 1/79 783). The bullfrog and macaque calls were kindly provided by Mark Bee and Asif Ghazanfar, respectively.