Perception of acoustic scale and size in musical instrument sounds
From CNBH Acoustic Scale Wiki
There is size information in natural sounds. For example, as humans grow in height, their vocal tracts increase in length, producing a predictable decrease in the formant frequencies of speech sounds. Recent studies have shown that listeners can make fine discriminations about which of two speakers has the longer vocal tract, supporting the view that the auditory system discriminates changes on the acoustic-scale dimension. Listeners can also recognize vowels scaled well beyond the range of vocal tracts normally experienced, indicating that perception is robust to changes in acoustic scale. This paper reports two perceptual experiments designed to extend research on acoustic scale and size perception to the domain of musical sounds: The first study shows that listeners can discriminate the scale of musical instrument sounds reliably, although not quite as well as for voices. The second experiment shows that listeners can recognize the family of an instrument sound which has been modified in pitch and scale beyond the range of normal experience. We conclude that processing of acoustic scale in music perception is very similar to processing of acoustic scale in speech perception.
Ralph van Dinther , Roy Patterson
Contents |
Introduction
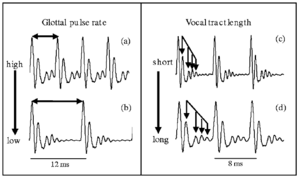
When a child and an adult say the same word, it is only the message that is the same. The child has a shorter vocal tract and lighter vocal cords, and as a result, the waveform carrying the message is quite different for the child and the adult. The form of the size information is illustrated in Fig. 1, which shows four versions of the vowel /a/ as in ‘hall’. From the auditory perspective, a vowel is a ‘pulse-resonance’ sound, that is, a stream of pulses, each with a resonance showing how the vocal tract responded to that pulse. The ‘message’ of the vowel is contained in the shape of the resonance (i.e. the relative height and spacing of the ripples following each pulse) which is the same in every cycle of all four waves of Fig. 1. The left column shows two versions of /a/ spoken by one adult using a high (a) and a low (b) pitch; the glottal pulse rate determines the pitch of the voice. The resonances are the same since it is the same person speaking the same vowel. The right column shows a child (c) and the same adult (d) speaking the /a/ sound on the same pitch. The pulse rate and the shape of the resonance are the same, but the scale of the resonance within the glottal cycle is dilated in the lower panel. The adult has a longer vocal tract which reduces the formant frequencies and the formant bandwidths. With the reduced formant bandwidths the resonances ring longer. Thus, vowel sounds contain two forms of information about the size of the source -- the pulse rate (PR) and the resonance scale (RS); the shape of the resonance carries the message.
A high-quality vocoder has been developed that can manipulate the PR and RS of natural speech (Kawahara et al., 1999; Kawahara and Irino, 2004); it is referred to as STRAIGHT and it has been used to manipulate the PR and RS of speech sounds in a number of perceptual experiments. For example, Smith et al. (2005) and Ives et al. (2005) used STRAIGHT to scale the resonances in vowels and syllables, respectively, and they showed that listeners can reliably discriminate the changes in RS that are associated with changes in vocal-tract length (VTL). Listeners heard the difference between scaled vowels as a difference in speaker size, and the just-noticeable-difference (JND) in perceived size was less than 10% for a wide range of combinations of PR and RS. Smith and Patterson (2005) also used STRAIGHT to scale the resonances in vowels and showed that listeners’ estimates of speaker size are highly correlated with RS. They manipulated the PR as well as the RS and found that PR and RS interact in speaker size estimates. Assmann et al. (2002) and Smith et al. (2005) showed that vowels manipulated by STRAIGHT are readily recognized by listeners. Assmann et al. showed that a neural net model could be used to explain the recognition performance provided the vowels were not scaled too far beyond the normal speech range. Smith et al. showed that good recognition performance is achieved even for vowels scaled well beyond the normal range. They argued that it was more likely that the auditory system had general mechanisms for normalizing both PR and RS, as suggested by Irino and Patterson (2002), rather than a neural net mechanism for learning all of the different acoustic forms of each vowel type, as suggested by Assmann and Neary (2002). We will return to the issue of mechanisms in the discussion (Section V). The purpose of the current study was to extend the research on the perception of scaled sounds to another class of everyday sounds where it is clear that source size plays a role in what we perceive. The sounds are the musical notes produced by the sustained-tone instruments of the orchestra. They come in families (e.g., brass instruments) which have similar shape and construction, and which differ mainly in size (e.g., trumpet, trombone, euphonium and tuba). We hear the members of a family as sounding the same in the sense of having the same timbre (the message), but at the same time we are able to tell whether the sound we are listening to is from a larger or smaller member of the family. Section II of this paper briefly reviews the form of size information in the notes of sustained-tone instruments, and the role of RS in the perception of musical sounds. The section shows that, although the mechanisms whereby musical instruments produce their notes are very different from the way humans produce vowels, the notes are, nevertheless, pulse-resonance sounds, and the information about instrument size is largely summarized in the PR and RS values. Section III describes an experiment on the discrimination of RS in sounds produced by four musical instruments taken from four families; strings, woodwinds, brass and voice. The just-noticeable-difference (JND) for the RS dimension is found to be a little larger for brass, string and woodwind instruments than it is for the voice (as an instrument). Section IV describes a recognition experiment for 16 musical sounds (four instruments in each of four families). The experiment shows how much the RS of an instrument can be modified without rendering the individual instruments unrecognizable. In both experiments, the scaling is implemented with STRAIGHT. Then in Section V, we return to the question of how the auditory system might process RS information in music and speech sounds.
Resonance scale in musical instruments
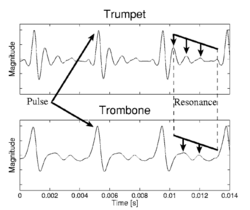
The waveforms of a trumpet and a trombone are shown in Fig. 2, which shows that they both have a pulse-resonance form.1 They also have the same PR, and so they are playing the same note (A#3, 233 Hz). The RS of the trombone is more dilated than that of the trumpet, and it is this that makes the trombone sound larger than the trumpet when they play the same note. Dilation in the time domain corresponds to contraction of the envelope in the frequency domain. In this section we briefly describe the mechanisms that control the PR and RS in instruments capable of producing sustained sounds. (Note that the human voice is a sustained-tone instrument, in this sense.) The purpose of the analysis is to illustrate the ubiquitous nature of size information in everyday sounds. First, we review the ‘source-filter’ model which is traditionally used to explain the sounds produced by sustained-tone instruments. Then, we show that scaling the spatial dimensions of an instrument proportionately produces waveforms whose structure is invariant, and which differ only in terms of the value of a scaling constant. This illustrates that scale is a property of sound, just like time and frequency (Cohen, 1993).2
Sustained-tone instruments
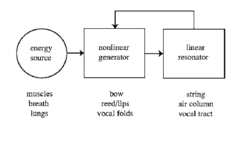
Musical instruments that produce sustained tones can be modelled as linear resonant systems (e.g., air columns, cavities, strings) excited by a nonlinear generator (e.g., vocal folds, lips, reeds, bows). The nonlinear generator produces acoustic pulses, and when the generator is coupled to the resonator, as indicated by the feedback loop in Figure 3, the system produces a temporally regular stream of acoustic pulses, similar to a click train.
Thus, the nonlinearity of the generator virtually ensures that the waves of sustained-tone instruments are pulse-resonance sounds (Benade 1976, Fletcher 1978, McIntyre 1983). A similar analysis applies to the voiced sounds of speech (Chiba and Kajiyama, 1942; Fant, 1960). The Fourier spectrum of a click train is a set of phase-locked harmonics of the click rate, and Fletcher (1978) has confirmed that the notes of sustained-tone instruments have overtones that are strictly harmonic up to fairly high harmonic numbers – locked to the fundamental both in frequency and phase.
The ‘source’ in sustained-tone instruments
The excitation source in stringed instruments is a combination of bow and string. Over the first 50 ms or so, the string forces the vibration produced by bowing into a standing wave with a quasi-sawtooth shape. Fourier analysis of this waveform shows a spectrum containing all harmonics of the fundamental, with amplitudes decreasing at approximately 6 dB/octave (Fletcher 1999). All of the harmonics are in phase, as indicated by the sharp rise at the start of each cycle of the sawtooth wave. The excitation of woodwind, brass and vocal instruments can be modelled by standard fluid mechanics, in terms of ‘valves’ that control the momentary closing of a stream of air. For woodwind instruments, the valve is the reed, for brass instruments, it is the lips, and for the voice, it is the vocal folds. The reeds of the saxophone and clarinet are designated ‘inward-striking’ valves Helmholtz (1877). The lips exciting brass instruments and the vocal folds exciting the vocal tract, are designated ‘outward striking’ or ‘sideways-striking’ valves (Fletcher and Rossing 1998). The pulsive nature of the excitation generated by reed, lip and vocal-fold vibrations, and the temporal regularity of the pulse stream, mean that the dominant components of the spectrum are strictly harmonic and they are phase locked (Fletcher and Rossing 1998). Fletcher (1978) provides a mathematical basis for understanding mode locking in musical instruments.
Spectra filtering in sustained-tone instruments
The spectral envelope of the source wave of a sustained-tone instrument is modified by the resonant properties of the instrument’s components. For stringed instruments, the prominent resonances are associated with the plates of the body (wood resonances), the body cavities (air resonances), and the bridge (Benade 1976). For brass and woodwind instruments, the prominent resonances are associated with the shape of the mouthpiece, which acts like a Helmholtz resonator, and the shape of the bell which determines the efficiency with which the harmonics radiate into the air (Benade 1976, Benade and Lutgen 1988). Woodwind instruments have a tube resonance like brass instruments, however, the spectrum is complicated due to the ‘open-hole cutoff frequency’. The dominant resonances of speech sounds are determined by the shape of the vocal tract (Chiba and Kajiyama, 1942; Fant, 1960). The important point in this brief review, however, is that these body resonances do not affect the basic pulsive nature of the sounds produced by sustained-tone instruments. In summary, the harmonic structure of the notes produced by sustained-tone instruments, and the fact that the components are phase locked, indicates that a simple model with a nonlinear pulse generator and a coupled linear resonator works quite well for these instruments, including the voice. From the point of view of the instrument maker and the physicist, the review emphasises that there are many ways to produce a regular stream of pulses and many ways to filter the excitation when producing music and speech. From the auditory perspective, these are pulse-resonance sounds which are characterized by a pulse rate, a resonance scale and a message which is the shape of the resonance.
The relation between resonance scale and the size of an instrument
If the three spatial dimensions of an instrument are increased by a factor, lambda, keeping the materials of the instrument the same, the natural resonances decrease in frequency by a factor of 1/lambda. The shape of the spectral envelope is preserved under this translation; the envelope simply expands or contracts by 1/lambda; on a log-frequency scale, the spectrum shifts as a unit without expansion or contraction. This scaling relationship is called ‘the general law of similarity of acoustic systems’ (Fletcher and Rossing, 1998). It is easy to confirm the law for simple vibrators such as the Helmholtz resonator or a flat plate. The natural frequency of a Helmholtz resonator is
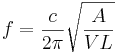(1)
If the spatial dimensions are scaled up by a factor λ, then
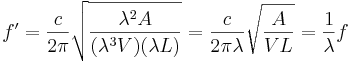(2)
The resonance frequencies of a plate with dimensions Lx and Ly and thickness h are
![f_{nm}=kh[(\frac{m}{L_x})^2 + (\frac{n}{L_y})^2]](../images/math/f/5/0/f50758f2c37d81efedb9476fbe271c1d.png)
(3)
where (n,m) are numbers of nodal lines in the y and x direction of the plate. Scaling of the spatial dimensions by a factor lambda results in
![f_{nm}'=k{\lambda}h[(\frac{m}{{\lambda}L_x})^2 + (\frac{n}{{\lambda}L_y})^2]=\frac{1}{\lambda}f_{nm}](../images/math/e/d/5/ed520b2e96c0e8763fb5229726a612dc.png)
(4)
Scaling the spatial dimensions of an instrument to produce another member of the family in a different register can result in an instrument which is too large, or too small, to play. To solve this problem, instrument makers often adjust the scale of the instrument by (a) changing the spatial dimensions less than would be required to achieve the register change, and at the same time, (b) changing some other property of the instrument that affects scale (such as the thickness, mass or stiffness of one or more of the components) to achieve the desired RS. In this way, they preserve the formant relationships without disproportionate scaling of the spatial dimensions. For example, Hutchins (1967, 1980) constructed a family of eight instruments covering the entire range of orchestral registers, based on the properties of the violin. If the dimensions of the contra bass were six times greater then those of the violin, the formant ratios of the contra bass body would be the same as those of the violin. However, a contra bass six times as large as a violin would be 3.6 m tall, which would be completely impractical. So, in the construction of the new family of violins, the body size and string lengths were scaled to fit human proportions, and the RSs and PRs required for the lower registers were obtained by adjusting the thickness of the body plates, the mass of the strings and the tension of the strings (Benade 1976). Similarly, the dimensions of the f-holes were adjusted to attain the required air resonance frequencies. So for the string family, the law of similarity is actually a law of similarity of shape; the spatial scale factors are smaller than would be required by a strict law of similarity; they have to be augmented by mass and thickness scaling to produce the formant ratios characteristic of the string family in an instrument with a large RS. The law of similarity also applies to brass instruments, and with similar constraints. Luce and Clark (1967) analyzed 900 acoustic spectra from a variety of brass instruments and showed that the spectral envelopes of the trumpet, trombone, open French horn and tuba were essentially scaled versions of one another, and Fletcher and Rossing (1998) report that the size of the cup scales roughly with the size of the instrument. However, the instrument makers adjust the shape of the bell beyond what would be indicated by strict spatial scaling to produce a series of harmonic resonances and to improve tone quality. So the notes of the different brass instruments in the experiment would be expected to differ mainly in PR and RS as dictated by the law of similarity, but also to a lesser degree to differences in bell shape. In summary, scaling the spatial dimensions of an instrument would shift the frequencies of the resonances in a way that would preserve formant frequency ratios and produce a family of instruments with the same timbre in a range of registers. Thus, when we change the RS of an instrument sound with STRAIGHT, the listener is very likely to perceive the sound as a larger or smaller instrument of the same family. For practical reasons, instrument makers achieve the desired RS for the extreme members of a family with a combination of spatial dimension scaling and scaling of other properties like mass and thickness. Thus, if listeners were asked to estimate the spatial size of instruments from sounds scaled by STRAIGHT, we might expect, given their experience with natural instruments, that they would produce estimates that are less extreme than the resonance scaling would produce if it were entirely achieved by increasing the spatial dimensions of the instrument. This means that the experiments in this paper are strictly speaking about the perception of acoustic scale in musical instruments. However, listeners do not have a distinct concept of scale separate from size, and they associate changes in acoustic scale with changes in spatial size, and so the experiments are about source size in the sense that people experience it. We will draw attention to the distinction between acoustic scale and size at points where it is important.
Resonance scale discrimination in musical instruments
The purpose of this experiment was to determine the just-noticeable-difference (JND) for a change in the resonance scale of an instrument over a large range of PR and RS. The experiment is limited to relative judgments about RS, and so the distinction between acoustic scale and source size does not arise; there is a one-to-one mapping between acoustic scale and source size in this experiment.
Method
Stimuli and experimental design
The musical notes for the experiments were taken from an extensive, high-fidelity database of musical sounds from 50 instruments recorded by Real World Computing (RWC) (Goto et al., 2003). This database provided individual sustained notes for four families of instruments (strings, woodwind, brass and voice) and for several members within each family. We chose these specific instrument families for two reasons: 1) They produce sustained notes, and so there is little to distinguish the instruments in terms of their temporal envelopes. 2) The sounds have a pulse-resonance structure and there is a high-quality vocoder that can manipulate the PR and RS in such sounds. The vocoder is referred to as STRAIGHT (Kawahara et al., 1999, 2004) and its operation is described below. In the database, individual notes were played at semitone intervals over the entire range of the instrument. For the stringed instruments, the total range of notes was recorded for each string. The notes were also recorded at three sound levels (forte, mezzo, piano); the current experiments used the mezzo level. The recordings were digitized into “wav” files with a sampling rate of 44100~Hz and 16-bit amplitude resolution.
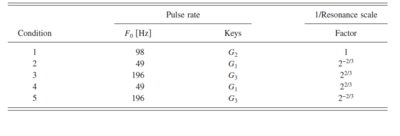
The first experiment focused on the baritone member of each instrument family: for the string family, it is the cello; for the woodwind family, the tenor saxophone; for the brass family, the French horn, and for the human voice, the baritone. Each note was extracted with its initial onset and a total duration of 350~ms. The onset of the recorded instrument was included to preserve the dynamic timbre cues of the instrument. A cosine-squared amplitude function was applied at the end of the waveform (50~ms offset) to avoid offset clicks. The notes were scaled using the vocoder, STRAIGHT, described by Kawahara et al. (1999; 2004). It is actually a sophisticated speech processing package designed to dissect and analyze an utterance at the level of individual glottal cycles. It segregates the glottal-pulse rate and spectral envelope information (vocal-tract shape information and vocal-tract length information), and stores them separately, so that the utterance can be resynthesized later with arbitrary shifts in glottal-pulse rate and vocal-tract length. Utterances recorded from a man can be transformed to sound like a woman or a child. The advantage of STRAIGHT is that the spectral envelope of the speech that carries the vocal-tract information is smoothed as it is extracted, to remove the harmonic structure associated with the original glottal-pulse rate, and the harmonic structure associated with the frame rate of the Fourier analysis window. For speech, the resynthesized utterances are of extremely high quality, even when the speech is resynthesized with PRs and vocal tract lengths beyond the normal range of human speech. Assmann and Katz (2005) compared the recognition performance for vowels vocoded by STRAIGHT with performance for natural vowels and vowels from a cascade formant synthesizer. They found that performance with the vowels vocoded with STRAIGHT was just as good with natural vowels, whereas performance was 9%-12% lower with the vowels from the cascade formant synthesizer. Liu and Kewley-Port (2004) have also reviewed the vocoding provided by STRAIGHT and commented very favorably on the quality of its resynthesized speech. STRAIGHT also appears to be a good ‘mucoder’ (i.e., a device for encoding, manipulating and resynthesizing musical sounds) for the notes of sustained-tone instruments where the excitation is pulsive. There are audio file examples available on our website to demonstrate the naturalness of the mucoded notes . STRAIGHT was used to modify the PR and RS of the notes required for the discrimination experiment, in which the JND was measured for five combinations of PR and RS as indicated in Table 1. The experiment was performed with short melodies instead of single notes to preclude listeners performing the task on the basis of a shift in a single spectral peak. The notes shown in this table indicate the octave and key of the tonal melodies presented to the listeners. Figure 4 shows the PR-RS plane and the points where the JND was measured; the arrows show that the JND was measured in the RS dimension. The stimuli were presented over headphones at a level of approximately 60~dB~SPL to listeners seated in a sound attenuated booth.
Auditory images of the stimuli
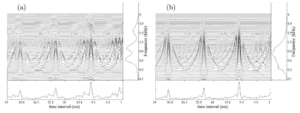
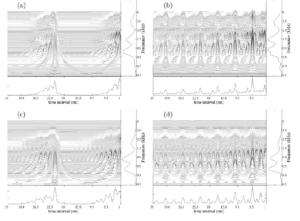
The effects of scaling the stimuli with STRAIGHT are illustrated in Figs 5, 6 and 7, using ‘auditory images’ of the stimuli (Patterson et al., 1992; 1995) that illustrate the form of the PR and RS information in the sound. The spectral and temporal profiles of the images provide summaries of the PR information from the RS information. Figure 5a shows the auditory image produced by the baritone voice with a PR of 98 Hz (G2) and the original VTL, that is, an RS value of 1. Figure 5b shows the auditory image for the corresponding French horn note. The auditory image is constructed from the sound in four stages: First, a loudness contour is applied to the input signal to simulate the transfer function from the sound field to the oval window of the cochlea (Glasberg and Moore 2002). Then a spectral analysis is performed with a dynamic, compressive, gammachirp auditory filterbank (Irino and Patterson, 2006) to simulate the filtering properties of the basilar partition. Then each of the filtered waves is converted into a neural activity pattern (NAP) that simulates the aggregate firing of all of the primary auditory nerve fibres associated with that region of the basilar membrane (Patterson, 1994a). Finally, a form of ‘strobed temporal integration’ is used to calculate the time intervals between peaks in the NAP and construct a time interval histogram for each of the filter channels (Patterson, 1994b). The array of time-interval histograms (one for each channel of the filterbank) is the auditory image; see Patterson et al. (1995, Fig. 2) for a discussion of the outputs of the different stages of processing. The auditory image is similar to an autocorrelogram (Meddis and Hewitt, 1991) but strobed temporal integration involves far less computation and it preserves the temporal asymmetry of pulse resonance sounds which autocorrelation does not (Patterson and Irino, 1998). The auditory image is the central ‘waterfall’ plot in Figs 5a and 5b; the vertical ridge in the region of 10 ms, and the resonances attached to it, provide an aligned representation of the impulse response of the instrument as it appears at the output of the auditory filterbank. The profile to the right of each auditory image is the average activity across time interval; it simulates the tonotopic distribution of activity in the cochlea or the auditory nerve, and it is similar to an excitation pattern. The unit on the axis is frequency in kHz and it is plotted on a quasi-logarithmic ‘ERB’ scale (Moore and Glasberg, 1983). The peaks in the spectral profile of the voice show the formants of the vowel. The profile below each auditory image shows the activity averaged across channel, and it is like a summary autocorrelogram (Yost et al., 1996) with temporal asymetry; the largest peak in the time-interval profile (in the region beyond about 1.25 ms) shows the period of the sound (G2; ~10ms), much as the first peak in the summary autocorrelogram shows the pitch of a sound (Yost et al., 1996). Comparison of the time-interval profiles for the two auditory images shows that they have the same PR, and thus the same temporal pitch (G2). Comparison of the spectral profiles shows that the voice is characterized by three distinct peaks, or formants, whereas the horn is characterized by one broad region of activity. The effect of STRAIGHT on the baritone voice is illustrated by the four panels in Fig. 6; they show how the auditory image changes when the PR and RS are altered to produce the values represented by the outer four stimulus conditions in Fig. 4. Comparison of the auditory image of the original baritone note in Fig. 5a with the images in the left-hand column of Fig. 6 shows that the PR has been reduced by an octave; the main vertical ridge in the image, and the largest peak in the time-interval profile (beyond 1.25 ms) have shifted from ~10 to ~20 ms. The panels in the right-hand column, show the images when the PR has been increased by an octave; the main ridge and the main peak now occur at ~5 rather than ~10 ms. Comparison of the time-interval profile for the original French horn note in Fig. 5b, with the time-interval profiles in the left-hand and right-hand columns of Fig. 7, shows the same effect on PR; that is, the rate is reduced by an octave for both panels in the left-hand column and increased by an octave in both panels of the right-hand column. Together the figures illustrate that the pitch of pulse resonance sounds is represented by the position of the main vertical ridge of activity in the auditory image itself, and by the main peak in the time-interval profile (beyond about 1.25 ms). Comparison of the auditory image of the original baritone note (Fig. 5a) with the images in the upper row of Fig. 6 shows the effect when STRAIGHT is used to reduce RS; the pattern of activity in the image, and the spectral profile, move up in frequency. For example, the second formant has shifted from about 0.9 to 1.2 kHz, although the vowel remains the same. In the lower row, the RS has been increased, with the result that the pattern of activity in the image, and the spectral profile, move down in frequency. Comparison of the original French horn note in Fig. 5b with the scaled versions in Fig. 7, shows the same effect on RS for the French horn; that is, the pattern moves up as a unit when RS decreases, and down as a unit when RS increases. Moreover, a detailed examination shows that the patterns move the same amount for the two instruments. Together the figures illustrate that the RS information provided by the body resonances is represented by the vertical position of the pattern in the auditory image. The auditory images and spectral profiles of the baritone voice notes in Fig. 6 and the French horn notes in Fig. 7 suggest that RS is a property of timbre. That is, the notes in each column of each figure have the same pitch, so if the notes were equated for loudness, then the remaining perceptual differences would be timbre differences, according to the usual definition. There are two components to the timbre in the current example, instrument family which distinguishes the voice notes from the horn notes, and instrument size which distinguishes the note in the upper row from the note in the bottom row, in each case. The two components of the timbre seem largely independent which supports the hypothesis that RS is a property of timbre. In this case, we might expect to find that listeners use RS to distinguish instruments, and since RS reflects the size of body resonances, we might expect listeners to hear RS differences as differences in instrument size. The question then arises as to how large a difference in RS is required to reliably discriminate two instruments, and this is the motivation for the discrimination experiment. The mathematics of acoustic scale lends support to the hypothesis that RS is a property of auditory perception; however, the mathematics indicates that RS is a property of sound itself, rather than a component of timbre. We will return to this topic in the Discussion. The purpose of the current experiment is to demonstrate that RS provides a basis for discriminating the relative size of two instruments on the basis of their sounds. It is not crucial to the design of the experiments or the interpretation of the results, whether RS is a property of timbre or an independent property of sound itself.
Procedure and listeners
A 2-interval forced-choice procedure was used to measure the JND for RS. Each trial consisted of two intervals with random tonal melodies played by one instrument. Short diatonic melodies were presented to convey the impression of tonal music and to preclude discrimination based on a simple spectral strategy, like tracking a single spectral peak. Each melody consisted of four different notes chosen randomly without replacement from the following five notes: Gi,Ai,Bi,Ci + 1, where i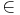 
{1,2,3} depended on the condition presented in Table 1. One of the stimulus intervals contained a melody with notes having a ‘standard’ RS value, while the other interval contained a melody with notes having a slightly larger or slightly smaller RS value. The order of the intervals was randomized. The listener's task was to listen to the melodies and indicate which interval contained the smaller instrument. Since a change in RS represents a proportionate change in the spatial dimensions of the instrument, it is reasonable to assume that the perceptual cue is closely related to the natural perception of a change in size, particularly since the scale differences within a trial were relatively small. No feedback was given after the response.
Psychometric functions were generated about the standard RS value using six modified RS values, three below the standard and three above the standard, ranging between factors of 2 − 1 / 2 to 21 / 2 for the cello, tenor sax and French horn, and between factors of 2 − 9 / 24 to 29 / 24 for the voice. The ranges were chosen following pilot listening to determine the approximate range of the psychometric function for each instrument. A run from one of the five conditions in Table~1 consisted of 240 trials (four instruments 
six points on the psychometric function 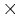ten trials); the order of the trials was randomized. Each psychometric function was measured four times, so each of the six points on the function was contrasted with the standard 40 times. The set of points describes a two-sided psychometric function showing how much the RS of the instrument has to be decreased or increased from that of the standard for a specific level of discrimination.
Four listeners, aged between 20 and 35, participated in the experiment. . There was one female and three males, all with normal hearing confirmed by an audiogram, and none of them reported any history of hearing impairment.
To familiarize the listeners with the task, a set of 50 trials was presented before each run. The RS differences in these trials were large to make discrimination easy.. During the training, feedback was given indicating whether the response was correct or incorrect; a trial was judged correct if the listener chose the sound with the smaller RS. The listeners had some difficulty with the cello, so several retraining trials were presented after every 90 trials of a run, to remind listeners of the perceptual cue.
Results and dicussion
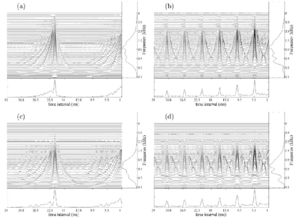
A sigmoid function was fitted to the discrimination data for each instrument, in each of the five experimental conditions set out in Table 1, to characterize the psychometric function for that condition. The full set of psychometric functions is shown in Fig. 8. The layout of the five panels in this figure corresponds to that shown in Fig. 4. The data from the four listeners all exhibited the same overall form and so the data were averaged over listeners. The solid, dashed, dotted and dashed-dotted lines represent the psychometric functions obtained for the cello, saxophone, French horn and baritone voice, respectively. The JND values for the four instruments are presented in the individual panels of Fig. 8. The JND was taken to be the percentage increase in RS required to support 76% correct performance on the psychometric function, or since the psychometric function is symmetric, the percentage decrease in RS required to support 24% correct performance. The JNDs for the baritone voice are the smallest; they are about 3% in the upper three panels, and rise to 10% in the lower, right-hand panel. The JNDs for the French horn are more uniform around 7%, while those for the saxophone are around 12%. The JNDs in the current experiment are largest for the cello. The JNDs are about 10% when the pitch is low and the instrument is small (or the pitch is high and the instrument is large) and they increase to around 20% when the pitch is low and the instrument is large (or the pitch is high and the instrument is small). In the central condition, the JND is about 15%. The rise in the JND along the positive diagonal from about 15-20% seems not unreasonable; in these conditions, the pitch rises as the instrument gets smaller (and vice versa) in the usual way, but these notes might be a little less familiar than those in the central condition. However, along the negative diagonal, the JND decreases from about 15 to about 10~%, in conditions where pitch rises as the instrument gets larger (and vice versa). We did not find any particular reason for this reversal of what might have been expected. The RS discrimination experiments of Smith et al. (2005) included conditions with a baritone voice and the JNDs are comparable to those observed in the current experiment. This includes the condition in the bottom right-hand panel of Fig. 8 where the JND rises to about 10%. The JNDs for sensory dimensions are typically 10% or more; in vision, the JND for brightness is around 14% (Cornsweet and Pinkster, 1956); in hearing, the JND for loudness is around 10% (Miller, 1947) and the JND for duration is around 10% (Able, 1972). The small JNDs associated with pitch and visual acuity are the exception. So, the JNDs for RS appear to be as good as, or slightly better than those for other auditory properties, which in turn supports the hypothesis that RS is a property of auditory perception. One of the listeners was an amateur musician who plays the viola da gamba. His JNDs for the cello were much smaller than those for the other listeners, whereas his JNDs for the other instruments were about the same, and so, familiarity with an instrument may improve performance. In summary, the results show that listeners are able to discriminate RS in instrument sounds. They can specify which is the smaller of two instruments from short melodies that differ in RS, and for the most part, they do not need feedback to support the discrimination. Within a family, the JND is fairly consistent, varying by no more than a factor of two across conditions, except for the baritone voice where it is a factor of three in one condition. Overall, listeners have slightly more difficulty when the instrument is large and plays a low-pitched melody.
Recognition of instruments scaled in PR and RS
The purpose of this experiment was to demonstrate that listeners can recognize versions of instrument sounds with a wide range of combinations of PR and RS; that is, listeners are robust to changes in RS as well as to changes in PR. The experiment includes PR and RS values within the normal range and beyond. Whereas Exp. I showed that listeners can discriminate changes in RS, Exp. II shows that listeners can recognize an instrument independent of its RS over quite a wide range of RS values.
Method
Stimuli and design
The same four instrument families were used in this experiment: string, woodwind, brass and voice. Four members with different sizes were chosen in each family; the specific instruments are presented in Table 2. The instruments in each row were chosen to have pitch ranges that largely overlap. For convenience, the four sizes are labeled by pitch range, or ‘register’, as ‘High’, ‘Mid-High’, ‘Low-Mid’ and ‘Low’. The instruments were selected from the RWC database (Goto et al., 2003), as before. Each note was extracted with its initial onset intact; the waves were truncated to produce a total duration of 350ms, and a cosine-squared gate was applied to reduce the amplitude to zero over the last 50ms of the sound. The use of natural sounds means that the notes contain cues such as vibrato and bow noise which can be used to recognize an instrument, in addition to the stationary pitch and timbre cues. In the selection of the sounds, we attempted to keep these cues to a minimum; however, one of the 16 instruments, the tenor voice, had a small amount of vibrato, which might be used as a recognition cue .
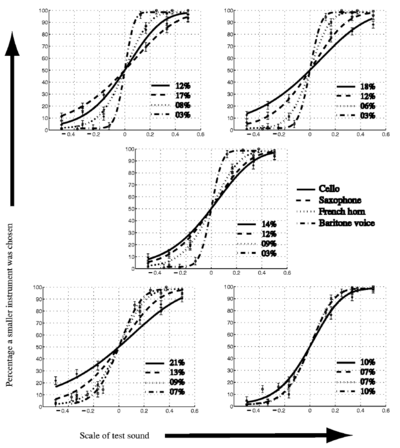
The vocoder STRAIGHT was used to modify the PR and the RS of the notes for all 16 instruments. The PR factors are presented in Table 3, along with the RS factors for each register in Table 2. The starting keys for the PR factors are indicated in the second column for each register. There were five PRs and five RSs, for a total of 25 conditions per instrument. Table 3 shows that the range of RS values is from 2 − 2 / 3 to 22 / 3, that is, each instrument was resynthesized as an instrument that was from 0.7 to 1.6 times the original RS. The PR range was from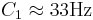 
to 
. The key, C1, is very close to the lower limit of melodic pitch, which is about 32Hz (Krumbholz et al., 2000; Pressnitzer et al., 2001).
Listeners and procedure
Four male listeners, aged between 20 and 35, participated in the experiment. Three of the four listeners also participated in Exp. I. They had normal hearing and they reported no history of hearing impairment. The stimuli were presented to the listeners over headphones at a level of approximately 60 dB SPL in a sound-attenuated booth. A 16-alternative, forced-choice procedure was used to measure recognition performance. On each trial, a note from one instrument was played three times; the note had one of five PRs and one of five RSs as indicated in Table 3. The listeners were presented with a graphical interface having 16 buttons labeled with instrument names in the layout shown in Table 2. The family name was presented above each column of buttons. The listeners' task was to identify the instrument from one of the 16 options. Feedback was presented at the end of each trial but only with regard to the family of the instrument. A run consisted of one trial for each instrument, of every combination of PR and RS; so there were 4 x 4 x 5 x 5 = 400 trials, and they were presented in a random order. Each listener completed 10 replications over a period of several days. At the start of each replication, the 16 instrument sounds were presented to the listeners twice; and then again after every 100 trials. Training was provided before the main experiment, to familiarize the listeners with the instrument sounds, and to see whether the listeners could identify the instruments prior to the experiment. The training was performed with the original notes rather than the notes manipulated by STRAIGHT. The training began with two families, namely, the woodwind and brass families. The notes of the two families were presented to the listeners twice. Then, the listener was tested with a mini-run of 32 trials, in which each of the eight instruments was presented four times. The trials had the same form as those in the main experiment, and there was instrument-specific feedback after each note. The train-and-test sessions were repeated until performance reached 90% correct. After one successful test run, the string family was added to the training set, and the train-and-test procedure was continued until performance returned to 90% correct for the three families. Then the final family, voice, was added and the training continued until performance returned to 90% correct for all four families. All of the participants completed the training successfully with three, or fewer, cycles of train-and-test at the three stages of training.
Results and discussion
The effects of PR and RS on instrument recognition
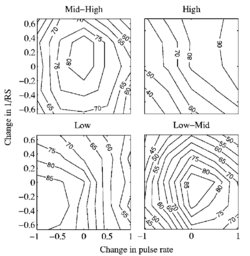
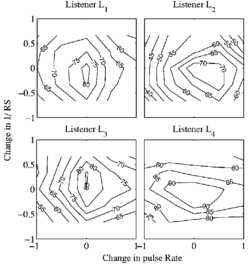
The pattern of recognition performance was similar for all four listeners; the mean data are presented in Fig. 9 as performance contours. Each data point is the percent correct instrument recognition for the 10 replications of each condition, averaged over the 25 conditions of PR and RS, the 16 instruments, and all four listeners – a total of 4 x 16 x 10 = 640 trials per point. The data are plotted on a base-2, logarithmic axis both for the change in PR (the abscissa) and the change in RS (the ordinate). The data for PRs with multiplication factors of 2 − 7 / 12 and 2 − 5 / 12 were averaged and plotted above the value 2 − 1 / 2 on the abscissa. Similarly, the conditions with multiplication factors 25 / 12 and 27 / 12 were averaged and plotted above 21 / 2. The contour lines show that performance is above 55% correct throughout the PR-RS plane, rising to over 80% correct in the center of the plane. This shows that listeners can identify the instruments reasonably accurately, even for notes scaled well beyond the normal range for that instrument. The chance level for this 16-alternative, instrument-identification task is about 6.25%; the chance level for correct identification of instrument family is about 25%; and when performance on the family-identification task is near 100%, then the chance level for instrument identification is closer to 25%. Either way, performance is well above chance throughout the PR-RS plane. Performance for notes with their original PR and RS values is a little below 90% correct for three of the four listeners, even though performance in the training sessions ended above 90% correct for all listeners. This is not really surprising since there were 400 different notes presented in each run. The effects of PR and RS were not uniform across the four registers, and so contour plots for the individual registers are presented in Fig. 10. The figure shows that the contour plots for the Mid-High and Low-Mid registers are similar to the contour plot of overall performance (Fig 9). But for the High register, peak performance is shifted to a higher PR and a smaller RS, and for the Low register, the effect is reversed -- peak performance is shifted to a lower PR and a larger RS. These results show that listeners are likely to choose the smallest instruments for combinations with a high PR and a small RS, and they are likely to choose the largest instruments for combinations with a low PR and a large RS. Contour plots for the individual listeners, averaged across conditions and instruments, are presented in Fig. 11. Performance is well above chance for all of the listeners throughout the plane, and the contours show that the surface is a smooth hill with its peak in the center for all listeners. Nevertheless, there are distinct differences between the listeners. The performance of listeners L1 and L3 is roughly comparable, with scores above 80% correct for the original notes in the center, falling to around 60% for the most extreme combinations of PR and RS values. For both listeners, the manipulation of PR produced a greater reduction in performance than the manipulation of RS. Listener L4 produced the best performance with greater than 90% correct over a large region around the original PR and RS values, and greater than 80% correct over most of the rest of the plane. Although this is probably due to musical training, it should be noted that this listener was the first author who prepared the stimuli for the experiment. For this listener, the manipulation of RS produced a greater reduction in performance than the manipulation of PR. Listener L2 produced the worst performance which was, nevertheless, above 70% for a substantial region near the center of the plane, and only fell to below 50% for the lowest PRs. For this listener, the manipulation of PR and RS have roughly similar effects. Two of the listeners were amateur musicians (L3 and L4) and the other two were non-musicians (L1 and L2). Table 4 provides a short description of each listener's musical involvement including their instrument, where appropriate, and their average percent correct for the original notes. The listener with the worst performance is a non-musician (L2) and the listener with the best performance is an amateur musician (L4) which suggests that there is a link between performance and musicality. However, L1 is a non-musician and this listener’s performance was comparable to that of L3 who was an amateur musician, indicating that the distributions are probably more overlapping than separate.
The effects of PR and RS on family recognition
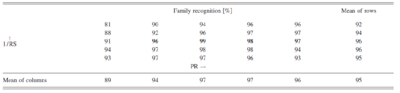
When listeners made a mistake in instrument identification, they typically chose a larger or smaller member of the same family whose PR and RS were compatible with those of the note they were presented. For example, when the PR of the viola was decreased and its RS increased, if the listener made an error, it was very likely that they would choose the cello as the instrument. Instrument-family recognition is analogous to vowel recognition; the four instrument families are like four vowel types. Within a family (e.g., brass) the notes of different instruments (e.g., the trumpet and tuba) are like tokens of one vowel (e.g., /i/) produced by people of different sizes (e.g., a small child and a large man, respectively). Accordingly, we reanalysed the data scoring a response correct if the instrument family was correct. The pattern of family recognition was similar for the four instrument families and so the data were averaged over family. The data are presented in Table~5, where family recognition is expressed as percent correct, averaged over listeners as well as families for the 25 conditions combinations of PR change and RS change. The rightmost column shows the mean RS values averaged over PR and the bottom row shows the mean PR values averaged over RS. Overall performance is 95 percent correct on family identification as shown in the bottom right-hand corner of the table. Thus, the vast majority of instrument errors are within-family errors. Moreover, performance is uniformly high at around 95 percent correct over much of the PR-RS plane. Thus, instrument family recognition is similar to vowel recognition in the sense that performance is very high over a large area of the PR-RS plane. Values below 95 percent correct are concentrated in the upper left section of the table where the PR and RS factors are both small. In this region, the instruments sound buzzy and the pitch for the low-register instruments falls below the lower limit of melodic pitch (Krumbholz et al., 2000; Pressnitzer et a., 2001). There were small differences between the instruments in this region; the average performance was roughly 70, 80, 90 and 100 percent correct, respectively, for the strings, brass, woodwinds and voice.
The tradeoff between PR and RS in within-family errors
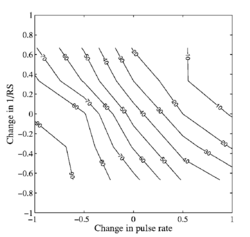
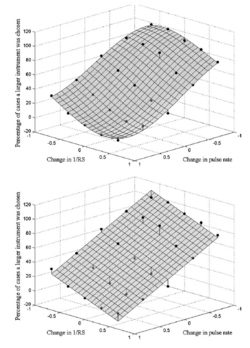
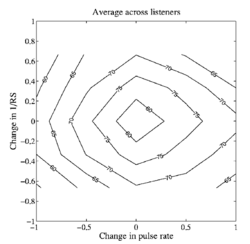
An analysis of the within-family, instrument-recognition errors is presented below with the aid of confusion matrices. The confusion data are highly consistent, so we begin by presenting a summary of the error data in terms of a surface that shows the trading relationship between PR and RS for within family errors. That is, given that the listener has made an error, in what percentage of these cases does the listener choose a larger member of the family, and how does this percentage vary as a function of the difference in PR and RS between the scaled and unscaled versions of the note? Figure 12 shows the results averaged over instrument family as a contour plot of within-family errors where the score is the percentage of cases where the listener chose a larger member of a family, given a specific combination of PR and RS. Consider first the 50% contour line. It shows that there is a strong trading relation between a change in PR and a change in RS. When we increase PR on its own, it increases the probability that the listener will choose a smaller member of the family; however, this tendency can be entirely counteracted by an increase in RS (making the instrument sound larger). Moreover, the contour is essentially a straight line in these log-log coordinates and the slope of the line is close to -1; that is, in log units, the two variables have roughly the same effect on the perception of which family member is producing the note. The same trading relationship is observed for all of the contours between about 20 and 80%, and the spacing between the lines is approximately equal. Together these observations mean that the errors are highly predictable on the basis of just two numbers, the logarithm of the change in PR and the logarithm of the change in RS. In an effort to characterize the trading relationship, we fitted a two-dimensional, third-order polynomial to the data of Fig. 12 using a least-squares criterion; the surface is shown with the data points in the top panel of Fig. 13. The data points are shown by black spheres and their deviation from the surface is shown by vertical lines. The surface fits the data points very well. The panel shows that the central section of the surface is essentially planar; the corners bend up at the bottom and down at the top due to floor and ceiling effects. The fact that the central part of the surface is planar means that we can derive a simple expression for the trading relationship that characterizes the data, except at the extremes, by fitting a plane to the data. The plane is shown with the data points in the bottom panel of Fig. 13. The fit is not much worse than that provided by the surface in the upper panel. The rms error increases a little from 13 to 30, but this is still relatively small, and the plane is described by three coefficients whereas the curved surface requires 10. The equation for the plane is z = − 38x − 30y + 50, where z is the ‘percentage of cases that a larger instrument was chosen’, x is log2(change in PR), and y is − log2((change in RS). The plane shows that, for any point in the central range, 1) an increase in PR of -0.5 log units (6 semitones) will increase the probability of choosing a larger instrument within the family by about 15%, and 2) a change in PR of $PR$ log units can be counteracted by a change in RS of 1.3PR log units. This means that, when measured in log units, the effect of a change in PR on the perception of size is a little greater than the effect of a change in RS. If we express the relationship in terms of JNDs instead of log units, the relative importance of RS increases. The JND for RS was observed in Exp. I to be about 10%. The JND for PR is more like 1% (Krumbholz et al., 2001; Figure 5). So, one JND in RS has about the same effect on the perception of size as 8 JNDs in PR.
Confusion matrices
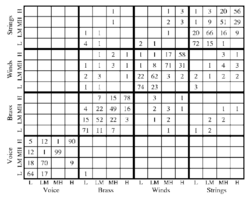
The confusion matrix for the 16 instruments in the experiment is presented in Fig. 14. The instrument presented to the listener is indicated on the abscissa by family name and register within family. The entries in each column show the percentage of times each instrument name was used in response to a given instrument on the abscissa (again by family and register). The entries are averaged over the 25 PRxRS conditions and over all four listeners. The figure shows that the majority of the responses are correct (68 %); they appear on the positive diagonal. Moreover, the diagonals immediately adjacent to the main diagonal contain 68 % of the remaining errors. So the most common error by far is a within family error to one of the instruments that is closest in size. The figure also shows that, away from the main diagonal, the errors still occur largely within family blocks. There are essentially no confusions between the human voice and the other instrument families; ‘voice’ is never used as a response when another instrument is presented, and ‘voice’ is always the response when a voice is presented. There is a low level of confusion between the remaining three instrument families, but it does not appear that any family confusion is more likely than any other. These family confusions also appear to be reasonably symmetric.
Source information for the recognition experiment
The stimuli in these experiments are natural sounds, and as such they could contain cues other than timbre, PR and RS which could be used to recognize an instrument. Although we chose the instruments and notes to minimize these extra cues, one of the 16 instruments, the tenor voice, had a small amount of vibrato. An analysis of the individual instrument data showed that performance for the tenor voice was somewhat better than for the other instruments (between 95-100% for all but the most extreme combinations of PR and RS), which suggests that the listeners probably did use the vibrato cue to assist in identifying this instrument. This was the only instrument for which performance was largely independent of PR and RS. For the other instruments, performance was lower and graded as illustrated in Figs 9 and 10. Figure 9 shows that performance decreases as PR and RS are manipulated from their initial values. Figure 10 shows that the effects of PR and RS were not uniform across the four registers. The contour plots for the High register show peak performance is shifted away from the center to a higher PR and a smaller RS. For the Low register, the effect is reversed. The results indicate that listeners’ judgments are strongly affected by the specific values of PR and RS, indicating that the extra timbre cues associated with the use of natural sounds did not dominate the judgments.
Discussion
The purpose of the current study was to extend previous research on the perception of scaled speech sounds to the perception of musical notes. The question arose following Cohen’s (1993) development of a transform to describe the scale information in sounds, such as the Doppler effect in echolocation, and the size related changes that occur in speech sounds as the vocal tract grows in length. Cohen has argued that ‘scale’ is a physical attribute of sound just like time and frequency. If this is the case, and if the auditory system has a general mechanism for processing acoustic scale, we might expect to find that (a) the fine discrimination of resonance scale observed with vowel sounds is also possible with the notes of sustained-tone instruments, since they also produce pulse-resonance sounds, and (b) listeners are able to recognize the family of an instrument from notes scaled in PR and RS over a wide range of PR and RS values.
Discrimination of RS in sustained-tone instruments
Smith et al. (2005) showed that listeners can discriminate a small RS difference between two vowel sequences, and Ives et al. (2005) showed that listeners can discriminate a small RS difference between two syllable phrases. They both interpreted the fact that the JND is small over a large portion of the PR-RS plane as supporting Cohen’s postulate that scale is a property of sound. Experiment I of the current paper showed that listeners are also able to discriminate a change in the RS of musical notes when presented two short melodies with slightly different RSs. The JND values are slightly larger than those obtained with speech sounds (Smith et al., 2005; Ives et al. 2005), and the JNDs are greater for some instruments than others, but they are on the same order as those for speech sounds (about 10 percent). Thus, discrimination of RS in the notes of sustained-tone instruments provides further support for the postulate that scale is a property of sound and that the auditory system has a mechanism for processing it.
Recognition of scaled instruments
Smith et al. (2005) showed vowel recognition is robust to changes in PR and RS over the normal range of experience, and well beyond the normal range. They argued that their data support the hypothesis of Irino and Patterson (2002) that the auditory system has general purpose mechanisms for normalizing the PR and RS of sounds before vowel recognition begins. This was contrasted with the hypothesis of Assmann and Neary (2002) that listeners learn vowel categories by experience; they had shown that a neural net could learn to recognise scaled vowels from within the range presented during training. The focus of the discussion was the pattern of recognition performance in the region of the PR-RS plane where the combination of PR and RS is beyond normal experience. Neural nets have no natural mechanism for generalizing to stimuli whose parameter values are beyond the range of the training data (LeCun and Bengio, 1995; Wolpert, 1996a, b); their success is largely attributable to interpolating between values of the training data. The performance of automatic speech recognition systems improves if the system is adapted to the speech of individual speakers by expanding or contracting the frequency dimension to fit the VTL of the speaker (Welling and Ney, 2002). Thus, human performance on scaled vowels might deteriorate in the region beyond normal experience if they were using a neural net for learning and recognition without prior normalization. A general purpose scaling mechanism does not depend on training, and any observed limitations on performance are assumed to arise from other constraints. In support of the statistical learning hypothesis, Assmann and Neary (2002) noted that performance does drop off somewhat for stimuli with combinations of PR and RS beyond normal experience; in response, Smith et al. (2005) pointed out the fall off in performance only occurs for extreme combinations of PR and RS, and that performance remains high in regions of the PR-RS plane well beyond normal experience. The purpose of this section of the Discussion, however, is not to try and decide between these two hypotheses concerning the recognition of scaled vowels and scaled musical notes. It seems likely that, even if there is a general mechanism that normalizes sound patterns before the commencement of recognition processing, there is also a statistical learning mechanism at the recognition level. Thus, the question is not ‘Which mechanism do we have?’ but rather ‘How do the two mechanisms work together to produce the performance we observe’. The purpose of this part of the Discussion, then, is to review the pattern of musical note recognition with respect to everyday musical experience, and to compare it with vowel recognition and vowel experience. There is a notable difference between the human vocal tract and other musical instruments in terms of our experience of resonance scale. Humans grow continuously, whereas instruments come in a limited number of fixed sizes. Constraints on the production and playing of musical instruments mean that the instruments of one class (e.g., French horn or violin) are all pretty similar in size. Thus, the distribution of resonance scales that we experience is concentrated on a small number of widely spaced values. We experience the voice from a distribution of vocal tract lengths that is relatively smooth and continuous. With regard to the PR-RS plane, our experience of an instrument family is limited to examples from a small number of horizontal bands that are relatively narrow in the RS dimension, one band for each instrument within the family. In Table 5, the bands that provide our experience of the 12 brass, string, and woodwind instruments are all represented by the four bold numbers in the centre row. Strictly speaking, when the RS of one of these instruments is scaled up or down, it leads to a new instrument (within the same family) whose notes are not part of everyday experience. The lowest PR is not in bold font because this PR was below the normal range for all of the instruments. Recognition for the voice family was essentially uniform over the plane, so it can simply be neglected in this discussion. The table shows that increasing or decreasing RS has very little effect on performance. There is a small reduction in performance for notes with the smallest RS (top row) but it is limited to notes with low PRs. Overall, performance for notes from novel instrument sizes is 95.6 percent correct, compared with 97.5 percent correct for the traditional instruments. Thus, the instrument data do not show the pattern that would be expected for a system based solely on statistical learning. They are more compatible with a general normalization mechanism. There is an additional aspect to this argument: When the notes of the highest instrument in each of the brass, string, and woodwind families are scaled down in RS to simulate a smaller instrument, the RS of the notes is beyond the normal range for that family, for all of the PR conditions. Similarly, when the notes of the lowest instrument in each family are scaled up in RS to simulate a larger instrument, the RS is beyond the normal family range for all PR conditions. The extent to which the notes were scaled beyond the normal range of the family in Exp. II, is about the same as the extent to which the vowels were scaled beyond the normal range of human speech in Smith et al. (2005). The pattern of recognition performance for the brass, string and woodwind instruments is like that of the vowels in Smith et al. (2005), inasmuch as near ceiling performance extends well beyond the range of normal experience. To achieve this level of recognition performance, a statistical learning mechanism would have to extrapolate well beyond its experience, which is not something that they can typically do. It seems more likely that the learning mechanism is assisted by a general normalization mechanism which makes the family patterns similar before learning and recognition.
Interaction of PR and RS in the perception of instrument size
When listeners made a mistake during instrument identification, they typically chose a larger or smaller member of the same family – a member whose PR and RS are compatible with those of the note they were presented. This suggests that much of the distinctiveness of instruments within a family is due to the combination of PR and RS in the notes they produce. Analysis of the confusion data indicated that there is a strong trading relationship between PR and RS; an increase in PR can be counteracted by an increase in RS and vice versa, in judgments of instrument size. Similar effects were observed by Fitch (1994) and Smith and Patterson (2005), both of whom found that the PR and RS of speech sounds interact in the estimation of speaker size and speaker sex. Interaction of PR and RS is also evident in the data of Feinberg et al. (2005), who investigated the influence of PR and RS on the size, masculinity, age and attractiveness of human male voices. They found that decreasing PR and increasing RS both increased the perception of size, and that a combination of a decrease in PR and an increase in RS has an even larger effect on the perception of size. Together these results suggest that the perception of size information in musical sounds is similar to that observed with speech sounds.
Size/scale information in other sources
The idea that sounds from physical sources contain scale information, and that the mammalian auditory system uses some form of Mellin transform to normalize sounds for scale was first proposed by Altes (1978). He was particularly interested in echolocation by bats and dolphins, and the fact that the Mellin transform would provide for optimal processing of linear, period-modulated signals. The magnitude information of the Mellin transform provides a representation of the source that is independent of the speed of the source relative to the observer. The phase information in the Mellin transform can be used to estimate the rate of dilation of the signal for echolocation. But Altes (1978) also recognised that there was scale information in speech sounds and that the Mellin transform might be useful for producing a scale-invariant representation of speech sounds. Recent studies have shown that there is RS information in a range of vertebrate communication sounds: for example, birds (Fitch 1999), deer (Fitch and Reby, 2001; Reby and McComb, 2003), lions (Hast, 1989), dogs (Riede and Fitch, 1999) and macaques (Fitch, 1997). Several of these papers also demonstrate that animals are sensitive to differences in RS and they interpreted RS as size information. For example, Fitch and Kelly (2000) showed that cranes attend to changes in the formant frequencies of species-specific vocalizations, and they hypothesised that the formants provide cues to body size. Reby and McComb (2003) showed that male red deer with a low fundamental frequency and a long vocal tract had a greater chance of reproductive success. Finally, Gazanfar et al. (2006) have recently reported that adult macaques presented with silent videos of a large and a small macaque, and a simultaneous recording of the call of a large or small macaque, look preferentially to the video that matches the sound in terms of macaque size. There are also studies to show that there is RS information in the sounds produced by inanimate objects other than musical instruments, and that humans perceive the RS information in terms of source size. Houben et al. (2004) showed that listeners can discriminate changes in the size of wooden balls from the sound of the balls rolling along a wooden surface. Grassi (2005) dropped wooden balls of different sizes (that acted as pulse generators) on baked clay plates (that resonated), and asked listeners to estimate the size of the ball. The size estimates were correlated with ball size but the form of the clay plate influenced the size estimates, so it is not really clear in this case how the resonance scale of the sound was controlled or perceived. It was also the case that the larger balls produced louder sounds which probably influenced the judgments as well. Finally, Ottaviani and Rocchesso (2004) synthesized the sounds of spheres and cubes of different sizes and demonstrated that listeners can discriminate changes in the volume of the object from the synthesized sounds. In summary, studies with animal calls and the sounds of inanimate sources support the hypothesis that the mammalian auditory system has a general purpose mechanism for processing the acoustic scale information in natural sounds.
Resonance scale: a property of timbre or a property of sound?
In Section III.A.2, it was noted that the auditory images and spectral profiles of the baritone-voice notes in Fig. 6 and the French-horn notes in Fig. 7 suggested that RS is a property of timbre, according to the standard definition. That is, two instruments from one family playing the same note (same pitch) with the same loudness would nevertheless be distinguishable by the difference in RS, and so RS is a component of timbre perception. It was also noted that, although the mathematics of acoustic scale supports the hypothesis that RS is a property of auditory perception, the mathematics indicates that RS is a property of sound itself, independent of the definition of timbre. We pursue this distinction briefly in this final sub-section of the Discussion. In mathematical terms, the transformation of a sound wave as it occurs in air into basilar membrane motion on a quasi-logarithmic frequency scale, is a form of wavelet transform involving a warping operator that has the effect of segregating the RS information from the remaining information in the sound, which is represented by the shape of the magnitude distribution in the spectral profile. In mathematical terms, the spectral profile is a covariant scale-timbre representation of the sound (Baraniuk and Jones, 1993; Baraniuk and Jones, 1995); that is, a representation in which the timbre information about the structure of the source is coded in the shape of the distribution, and the RS information is coded, separately, in terms of the position of the distribution along the warped-frequency dimension. The importance of the covariance representation is the demonstration that the two forms of information can be segregated, because once segregated, the RS can be separated from the magnitude information using standard Fourier techniques. Moreover, the resulting magnitude distribution is a scale invariant representation of the timbre information (Baraniuk and Jones, 1993; Baraniuk and Jones, 1995). For example, Irino and Patterson (2002) have shown how the two-dimensional auditory image can be transformed into a two-dimensional, scale-covariant, Size Shape Image (SSI), and then subsequently, into a two-dimensional, scale-invariant, Mellin Image. They illustrated the transforms with vowel sounds, but the sequence of transformation would be equally applicable to the notes of sustained-tone instruments. The details of these alternative mathematical representations of sound, and their potential for representing auditory signal processing, are beyond the scope of this paper. The important point for the current discussion about timbre is that the mathematics indicates that acoustic scale is actually a property of sound itself (Cohen, 1993). This suggests that acoustic scale might better be regarded as a separate property of auditory perception, rather than an internal property of timbre. Just as the repetition rate of a sound is heard as pitch and the intensity of the sound is heard as loudness, so it appears that the acoustic scale of a sound has a major effect on our perception of the size of a source. Acoustic scale is not the only contributor to the perception of source size; clearly, the average pitch of the voice contributes to speaker size, and the average pitch of an instrument contributes to the perception of its size. Nevertheless, isolated changes in resonance scale are heard as changes in source size. In order to interpret acoustic scale information in terms of speaker size or instrument size, the listener has to have some experience with people and instruments, but the mapping between acoustic scale and resonator size is very simple in speech and music. The relationship between acoustic scale and VTL is essentially linear, and speaker size is very highly correlated with speaker height (Fitch and Giedd, 1999). Similarly, acoustic scale is linearly related to resonator size in musical instruments which is directly related to overall instrument size. For practical reasons, instrument makers choose to achieve some of the resonance scaling by means of changes in mass and thickness, but there remains a very high correlation between RS and instrument size within instrument families. So it is not surprising that the RS appears to function as a property of auditory perception like pitch and loudness, and not just a component of timbre. The purpose of this paper was to illustrate that RS provides a basis for size discrimination in instrument sounds, and that appropriate processing of RS information minimizes cross family confusion. It is not crucial to the design of the experiments or the interpretation of the results, whether the mathematics of acoustic scale eventually leads to a modification of the definition of timbre to exclude RS. Such a change in perspective would, however, appear to be worth considering given that we perceive instrument sounds in terms of families and members within families which differ in terms of their register. Part of the register information is average pitch, but another important part is resonance scale, and like pitch, resonance scale appears to function as a property of auditory perception.
Conclusion
Listeners can detect relatively small changes (about 10%) in the resonance scale of the notes produced by sustained-tone instruments, such as the instruments in the string, woodwind, brass and voice families. Listeners are also able to recognize instrument sounds scaled over a wide range of pulse rates and resonance scales, including combinations beyond the normal range. Both pulse rate and resonance scale contribute to the perception of instrument size, as expected, and there is a strong trading relationship between pulse rate and resonance scale in instrument identification. The results of the experiments suggest that pulse rate and resonance scale play similar roles in the perception of speech and music. As such, the results support the hypothesis that the auditory system applies some kind of scale transform to all sounds, to segregate the RS information and produce scale covariant and/or scale invariant representations of the sound source – representations that would be expected to enhance recognition performance (e.g., Welling and Ney, 2002).
Acknowledgements
We would like to thank the associate editor and the reviewers for their helpful comments. The research was supported by the U.K. Medical Research Council (G9901257, G9900369, G0500221), and ONRIFO (Grant N00014-03-1-1023).
References
LeCun, Y., and Bengio, Y. (1995). “Convolutional networks for images, speech, and time-series,” in The Handbook of Brain Theory and Neural Networks, (M. A. Arbib, ed.), MIT Press.
Wolpert D. H. (1996a). “The lack of a priori distinctions between learning algorithms,” Neural Computation 8, 1341-1390.
Wolpert, D. H. (1996b). “The existence of a priori distinctions between learning algorithms,” Neural Computation 8, 1391-1420.
