PGWshar10.4
From CNBH Acoustic Scale Wiki
Roy Patterson , Etienne Gaudrain, Tom Walters
Contents |
4. The Auditory Representation of Pulse-Resonance Sounds and Acoustic Scale
This section presents a brief description of a time-domain model of auditory perception to show how the auditory system constructs our internal representation of musical tones, and to illustrate how the acoustic scale variables appear in this representation of sound. The internal representation is referred to as an auditory image and the stages of the auditory model are intended to simulate all of the auditory processing required to transform a sound into our initial perception of that sound (Patterson et al. 1992; Patterson et al. 1995). The processes are analogous to those that the visual system uses to convert light entering the eye into an initial visual image of that light. Although the algorithms used to simulate the construction of the auditory image are straightforward in signal processing terms, auditory models are not commonly used to explain the perception of tones in music and speech research. The most common representation of sound in these research communities is the spectrogram, which is a temporally ordered sequence of magnitude spectra. The spectrogram is a linear-time, linear-frequency representation of sound, and it is normally plotted with time on the abscissa (x axis) and frequency on the ordinate (y axis) so that time progresses from left to right as the sound progresses. This section begins with a comparison of two auditory images (shown in Fig. 2) which illustrate the essentials of the auditory image as it pertains to the perception of musical tones, and how this representation of sound differs from the spectrogram.
4.1 Auditory Images
There are now a number of time-domain models of auditory processing that attempt to simulate the neural response to complex sounds like musical notes at a succession of stages in the auditory pathway, and which produce representations of sound that might be regarded as auditory images (e.g. Slaney and Lyon 1990; Meddis and Hewitt 1991; see de Cheveigné 2005 for a review). In these models, the auditory image is typically constructed in four stages which respectively simulate the operation of (i) the outer and middle ear, (ii) the basilar partition, (iii) the inner hair cells along the basilar partition, and (iv) the temporal integration mechanism in the mid-brain. The Auditory Image Model (AIM) (Patterson et al. 1992; Patterson et al. 1995) will be used to illustrate the construction of auditory images and the form of acoustic scale information in the image, as we currently understand it. What differs from one time-domain model to another is the degree to which they attempt to simulate the details of auditory processing in each stage, and the theoretical bases for the mechanisms chosen to represent these auditory processes. The differences are not particularly important for present purposes, since the section is just intended to illustrate the general form of the internal representation of sound and the form of the acoustic scale variables in the internal representation.
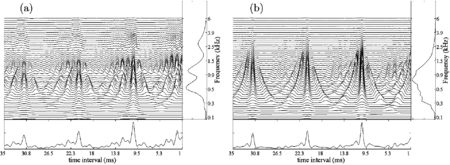
The auditory image of a baritone singing the vowel /a/ on the note G2 is presented in Figure 2a, and for comparison, the auditory image of a French horn playing the same note is shown in Figure 2b; the figure is reproduced from van Dinther and Patterson (2006) which provides a more detailed description of the image construction process. The auditory images are the large, two-dimensional, ‘waterfall’ plots; the dimensions of the auditory image are time-interval on the abscissa (from 1-35 ms increasing towards the left) and frequency on the ordinate (from 0.1 to 6.0 kHz). The properties of the auditory image will be introduced with reference to the four stages of processing used to construct them, and the aspect, or aspects of the auditory image that each stage of processing imparts to the image. The vertical profiles to the right of each image, and the horizontal profile below each image, will be introduced once the description of the auditory image itself is complete. [There are multi-panel figures in van Dinther and Patterson (2006) which show how the auditory images in Figure 2 were constructed, and how they change as the acoustic scale of the source and the acoustic scale of the filter vary.]
The first stage of processing simulates the effect of the outer and middle ear on incoming sound as it travels from the air through to the cochlea. It is these structures that determine the lower and upper frequency limits for human hearing in young normal listeners. Accordingly, from the perspective of music perception, the first stage determines the range of frequencies that young people normally hear, which is from about 0.1 to 12 kHz. The vertical dimension of the auditory image is the frequency dimension and so the first stage of processing determines the upper and lower bounds of the auditory image and how activity dies away as it approaches the edges of the image. In AIM, the weighting function is based on the loudness model of Glasberg and Moore (2002). In the case of speech and music, there is very little energy in the region above about 6 kHz, and what is there has very little effect on our perception of musical tones and speech sounds, so the plot of the auditory image is normally limited to 6 kHz as in the images presented in Figure 2.
The second stage of processing simulates the spectral analysis performed in the cochlea by the basilar membrane in conjunction with the outer hair cells and the tectorial membrane; these structures are collectively referred to as the “basilar partition”. The spectral analysis creates the tonotopic dimension along the basilar partition, and it creates the acoustic frequency dimension of auditory perception shown as the vertical dimension in the auditory image. In AIM, as in most time-domain models of perception, the spectral analysis is simulated with a bank of “auditory filters”. Each filter creates a “frequency channel” in the auditory image; that is, the filter passes acoustic energy in a small frequency region about its “centre frequency”, and outside this “pass-band”, the filter progressively attenuates acoustic energy as the frequency of that energy diverges from the centre frequency of the filter. This is the essence of an auditory filter. The width of the pass-band of the auditory filter increases with its centre frequency, and the spacing of the filters along the frequency dimension increases with centre frequency. As a result, the tonotopic dimension of the cochlea is a quasi-logarithmic frequency axis as shown in the auditory images of Figure 2. In the current version of AIM, the auditory filter is the compressive, gammachirp auditory filter (Irino and Patterson 2001; Patterson et al. 2003).
Each of the lines in the auditory image shows the recent history of activity in a specific frequency channel; the vertical position of the low-level activity in the channel shows the centre frequency of each filter. The activity in adjacent channels is correlated and, as a result, the set of filter outputs gives the visual impression of a surface in auditory image space. The surface is AIM’s simulation of the internal representation of sound that is assumed to be the basis of one’s initial perception of a sound. The tones of music produce distinctive structures in the auditory image as illustrated in Figure 2; the structures are referred to as “auditory figures” because they stand our like figures when presented in background noise (Patterson et al. 1992). The tonotopic dimension of the auditory image is similar to the frequency dimension in Figure 1b insofar as it is quasi-logarithmic; it differs from the strictly logarithmic frequency dimension of Figure 1b inasmuch as the density of channels decreases somewhat below about 0.5 kHz (e.g. Moore and Glasberg 1983).
In the current version of AIM, the auditory filter is the compressive, gammachirp auditory filter (Irino and Patterson 2001; Patterson et al. 2003). For readers with an interest in the details, the gammachirp auditory filter is a development of the gammatone auditory filter (Patterson et al. 1995; Unoki et al. 2006). The gammatone filter is essentially symmetric and it is linear, that is, it does not change shape with stimulus level. The gammachirp auditory filter is asymmetric and the asymmetry varies with stimulus level, as dictated by human masking data (Unoki et al. 2006). In the dynamic version of this gammachirp filter (Irino and Patterson 2006), a form of fast-acting compression is incorporated into the auditory filter itself. The compression responds to level changes within the individual cycles of pulse-resonance sounds and, as a result, the filter restricts the amplitude of the pulse and amplifies the resonance relative to the pulse in each cycle (see Irino and Patterson 2006, Fig. 7 and 9).
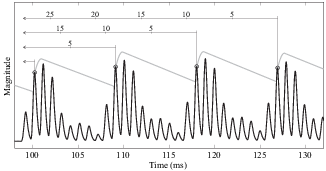
The third stage of processing simulates neural transduction, that is, the conversion of basilar partition motion into neural activity in the cochlea at the input to the auditory nerve. In AIM, neural transduction is assumed to take place separately in each frequency channel. Specifically, the ‘amplitude versus time’ wave that flows out of each auditory filter is (i) half-wave rectified (that is, the negative values are set to zero) and (ii) low-pass filtered to simulate the upper limit on the firing rate of auditory nerve fibres. The result is a simulation of the aggregate firing of all of the primary auditory nerve fibres associated with that region of the basilar membrane (Patterson 1994a); this function is referred to as a Neural Activity Pattern (NAP). The rapidly oscillating function in Figure 3 shows the NAP flowing from a single auditory filter in response to an /a/ vowel with a GPR of 116 cps and a period of 8.6 ms. The auditory filter is centered just above 1.0 kHz, so the individual cycles of the NAP are just under 1 ms in duration. Each cycle of the vowel produces a distinct cycle of activity in the NAP. There is one of these NAP functions for each of the filters in the filterbank and together they simulate the response of the cochlea to the vowel.
The fourth stage simulates the auditory temporal integration and it converts the set of NAP functions flowing from the auditory filterbank into AIM’s simulation of our auditory image of a sound, that is, the neural representation that forms the basis of what we perceive when presented with a sound. In auditory models, this fourth stage of processing is currently hypothetical, in the sense that we do not precisely know how or where it is performed. The reason why perceptual models require a fourth stage is because the time scale of level variation in the NAP functions is not compatible with our perception of sounds; it is clear that there must be some form of temporal integration in the system prior to the neural representation that is the basis of perception. Consider the NAP function in Figure 3: It shows the response to a little over three cycles of the vowel (a total duration of only 0.03 seconds), so a one second segment of the vowel with 116 cycles would be about 30 times the length of the segment shown in Figure 3. If Figure 3 were a real-time display (like the neural representation that we perceive), these 30 cycles of the NAP would flow very rapidly from right to left across the display in the course of one second, and it would just be a blur. So if the NAP functions were the basis of perception, we would not be able to use the fine-grain temporal information in the NAP functions. However, perceptual research on pitch and timbre indicates that at least some of the fine-grain, time-interval information in the NAP functions is preserved in the auditory image (e.g. Krumbholz et al. 2003; Patterson 1994a, 1994b; Yost et al. 1998). This means that the temporal integration process used to construct the auditory image cannot be simulated by a running temporal average process, like that used to construct the spectrogram because an averaging process would blur the temporal fine structure within the averaging window (Patterson et al. 1992, 1995).
Patterson et al. (1992) argued that it is the fine-structure of periodic sounds that is preserved rather than the fine-structure of aperiodic sounds (e.g. noises), and they showed that the fine-structure of periodic sounds could be preserved by a form of ‘strobed temporal integration’ controlled by an adaptive threshold. The adaptive threshold for the vowel NAP in Figure 3 is shown by the line with grey dots above the NAP function. It is a form of temporal envelope which emphasizes where the individual cycles of the NAP function start (the dots). These strobe points are used to direct the temporal integration process as indicated by the vertical lines and horizontal arrows above each strobe point. As the start of each new cycle of the NAP function is identified (the dots), a section of the NAP function from the strobe point back to 35 ms prior to the strobe point (the horizontal lines), is copied and added as a unit into the corresponding channel of the auditory image. In the process the strobe time in the NAP function is subtracted from absolute time in the NAP and so, in the auditory image, the activity associated with any given strobe extends from 0 ms in the auditory image (Fig. 2), backwards for 35 ms. Since the activity in successive cycles is very similar for pulse-resonance sounds, successive cycles sum to produce a stabilized representation of the pattern in the NAP.
The set of all image channels (one for each filterbank channel) is AIM’s representation of our internal auditory image, and the auditory images in Figure 2 were constructed in this way (Patterson 1994a, 1994b; Patterson et al. 1992, 1995). The image decays fairly slowly with respect to the rate of cycles in pulse-resonance sounds (specifically with a half life of 30 ms). So a stabilized version of the neural pattern within the cycle of the sound builds up in the auditory image when the sound comes on and stays there as long as the sound is stationary. When the sound goes off, it decays away to nothing in about 100 ms.
More detailed descriptions of auditory image construction are presented Patterson et al. (1995), van Dinther and Patterson (2006) and Ives and Patterson (2008). The auditory image is similar in form to the ‘autocorrelogram’ (Slaney and Lyon 1990; Meddis and Hewitt 1991; Yost 1996) but the construction of the auditory image is more efficient and it preserves the temporal asymmetry of pulse-resonance sounds. The similarities and differences between auditory images and autocorrelograms are described in Patterson and Irino (1998).
4.1 The Spectral Profile and Sf
While the processing of pulse-resonance sounds up to the level of our initial perception of them may seem complicated, the relationship between the acoustic properties of these sounds, as observed in their waves and log-frequency spectra, and the features that appear in the auditory images of pulse-resonance sounds is relatively straightforward. In Figure 2, the spectral profile to the right of each auditory image is the average of the activity in the image across time intervals; it simulates the tonotopic distribution of activity observed in the cochlea and in neural centers of the auditory pathway up to auditory cortex. The frequency axis is quasi-logarithmic like the tonotopic dimension of the cochlea (Moore and Glasberg 1983). The spectral profile of the auditory image is similar to the ‘excitation pattern’ described by, for example, Zwicker (1974) and Glasberg and Moore (1990), inasmuch as they all simulate the distribution of activity along the tonotopic axis in the auditory system with a compressed measure of magnitude.
The three peaks in the spectral profile for /a/ (G2) of the baritone in Figure 2a show the formants of this vowel. Note, that the profile from AIM is similar to the envelope of the magnitude spectrum of the child’s vowel, shown Figure 1b, except that the pattern in Figure 2a is shifted towards the origin with respect to that in Figure 1b because in Figure 2a, the singer is an adult.
The spectral profile of the auditory image is similar in form to the envelope of the magnitude spectrum. Both are covariant representations of family and register information (van Dinther and Patterson 2006); the family information is contained in the shape of the envelope, and register information is in the position of the envelope, Sf, along the frequency axis. Comparison of the spectral profiles of the auditory images in Figures 2a and 2b show that, whereas the spectral envelope of the voice is characterized by three distinct peaks, or formants, the envelope of the French horn is characterized by one broad region of activity.
4.2 The Time-Interval Profile and Ss
The resolution of the auditory filter, at the sound levels where we normally listen to music, is not sufficient to define individual harmonics of pulse-resonance sounds beyond the first three or four harmonics (e.g. Ives and Patterson 2008). As a result, the fine structure of the magnitude spectrum and Ss are not readily apparent in the spectral profile of the auditory image for musical sounds. However, the Ss information is present in the auditory image, in the form of the vertical ridge in the 10-ms region of the image. The ridge shows that there is a concentration of activity at the period of the tone in most channels of the auditory images in Figures 2a and 2b. Thus, the acoustic scale of the source is readily observed in this simulation of the neural representation of sound, even though the construction of the auditory image includes a temporal integration process with a half life of 30 ms. This is because strobed temporal integration preserves the temporal fine structure of periodic components of sounds like the sustained parts of vowels and musical notes.
Moreover, the temporal information associated with the acoustic scale of the source is enhanced in the time-interval profile of the auditory image. This profile appears below the auditory image and shows the activity averaged across filter channels. In this time-interval profile, the position of the largest peak (in the region to the left of 1.25 ms) provides an accurate estimate of the period of the sound (for G2, 10.2 ms). Moreover, the height of the peak, relative to the level of the background at the foot of the peak, provides a good measure of the salience of the pitch percept (Yost et al. 1996; Patterson et al. 2000; Ives and Patterson 2008). Thus, in time-domain models involving auditory images, the most obvious correlate of the acoustic scale of the source, Ss, in an instrument is a concentration of time intervals at a particular value in the temporal profile. This form of Ss information is more like the time between peaks in the sound wave (Fig. 2a) rather than the position of the fine structure in the magnitude spectrum of the sound (Fig. 2b).
4.3 Summary of Auditory Image Construction and the Acoustic Scale Information in the Image
In auditory models of perception, the auditory image which simulates the neural substrate of perception is typically constructed in four stages: A spectral weighting function, similar to the audiogram in form, simulates the middle-ear filtering that limits sensitivity to very high and very low frequencies. An auditory filterbank simulates the spectral analysis performed in the cochlea. Neural transduction is simulated with half-wave rectification and low-pass filtering. A sophisticated form of temporal integration stabilizes the repeating neural patterns produced by pulse-resonance sounds and completes the construction of the auditory image.
The main vertical ridge in the auditory image, and the corresponding peak in the time-interval profile, are the auditory model’s representation of the acoustic scale of the source, Ss. They move left to longer time intervals as the pulse rate of the sound decreases, and to the right to shorter time intervals as the pulse rate increases. When this Ss marker stands out clearly in the time-interval profile well above the background activity, the sound is effectively periodic and the tone is heard to have a strong pitch. When the scale of the filter, Sf, changes, the complex pattern in the auditory image simply moves up or down in frequency without changing shape. Similarly, the distribution of activity in the spectral profile of the image moves up or down without changing shape.